
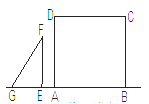
【题目】如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示的位置出发,沿直线AB向右匀速运动,当点G与点B重合时停止运动,设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是( )
A. 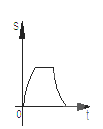 B.
B. 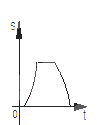 C.
C. 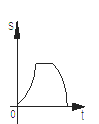 D.
D. 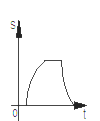
【答案】D
【解析】试题分析:设GE=a,EF=b,AE=m,AB=c,Rt△EFG向右匀速运动的速度为1,
当E点在点A左侧时,S=0。
当点G在点A左侧,点E在点A右侧时,如答图1,

AE=t﹣m,GA=a﹣(t﹣m)=a+m﹣t,
∵PA∥EF,∴△GAP∽△GEF。
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∴![]() 。
。
∴S是t的二次函数,且二次项系数为负数,所以抛物线开口向下。
当点G在点A右侧,点E在点B左侧时,S=![]() ab。
ab。
当点G在点B左侧,点E在点B右侧时,如答图2,

GB=a+m+c﹣t,
∵PA∥EF,∴△GBP∽△GEF。
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∴![]() 。
。
∴S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上。
综上所述,S与t的图象分为四段,第一段为x轴上的一条线段,第二段为开口向下的抛物线的一部分,第三段为与x轴平行的线段,第四段为开口先上的抛物线的一部分。
故选D。


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工业废气年排放量为400万立方米,为改善大气环境质量,决定分二期投入治理,使废气的年排放量减少到256万立方米,如果每期治理中废气减少的百分率相同.求每期减少的百分率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com