
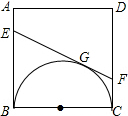
 如图,正方形ABCD的边长为a,以BC为直径向正方形内画半圆,EF切半圆于点G,分别交AB、CD于点E、F.
如图,正方形ABCD的边长为a,以BC为直径向正方形内画半圆,EF切半圆于点G,分别交AB、CD于点E、F.分析 (1)先判断BA、CD都与半圆相切,再根据切线长定理得到EB=EG,FG=FC,锐角利用等线段代换可得四边形AEFD的周长=AB+CD+AD=3a;
(2)作FH⊥BE于H,如图,则四边形BCFH为矩形,HF=BC=a,BH=FC,在Rt△EHF中利用含30度的直角三角形三边的关系得到EH=$\frac{\sqrt{3}}{3}$FH=$\frac{\sqrt{3}}{3}$a,EF=2EH=$\frac{2\sqrt{3}}{3}$a,接着利用等线段代换得到四边形EBCF的周长=2EF+BC,于是得到四边形EBCF的周长=$\frac{4\sqrt{3}+3}{3}$a.
解答 解:(1)∵以BC为直径向正方形内画半圆,EF切半圆于点G,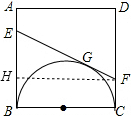
∴BA、CD都与半圆相切,
∴EB=EG,FG=FC,
∴四边形AEFD的周长=AE+EF+DF+AD=AE+EG+GF+DF+AD=AE+EB+FC+FD+AD=AB+CD+AD=3a;
(2)作FH⊥BE于H,如图,则四边形BCFH为矩形,HF=BC=a,BH=FC,
在Rt△EHF中,∵∠BEF=60°,
∴EH=$\frac{\sqrt{3}}{3}$FH=$\frac{\sqrt{3}}{3}$a,EF=2EH=$\frac{2\sqrt{3}}{3}$a,
∴四边形EBCF的周长=EB+EF+CF+BC
=EG+EF+FG+BC
=2EF+BC
=$\frac{4\sqrt{3}}{3}$a+a
=$\frac{4\sqrt{3}+3}{3}$a.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了切线长定理和正方形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
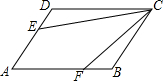 在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为$\frac{9}{5}$.
在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为$\frac{9}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.2×1010 | B. | 0.82×1011 | C. | 82×109 | D. | 8.2×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
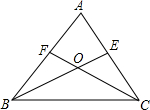 如图,BE、CF是△ABC的角平分线,BE、CF相交于点O.
如图,BE、CF是△ABC的角平分线,BE、CF相交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com