
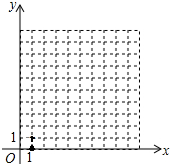
 如图,在平面直角坐标系中,一只蜘蛛P从点A(1,0),选择以下规定动作爬行
如图,在平面直角坐标系中,一只蜘蛛P从点A(1,0),选择以下规定动作爬行分析 (1)①爬行规律,可得每次爬行横坐标增加2,纵坐标增加1,可得答案;②根据爬行规律,可得每次爬行横坐标增加2,纵坐标增加2,可得答案;
(2)①根据先向右爬行2个单位长度,再向上爬行1个单位长度,可得横坐标是纵坐标的2倍,根据起点是(1,0),可得横坐标比纵坐标的2倍多1;
②根据先向右爬行2个单位长度,再向上爬行2个单位长度,可得横坐标与纵坐标相等,根据起点是(1,0),可得横坐标比纵坐标多1;
(3)根据先向右爬行2个单位长度,再向上爬行1个单位长度,可得每次爬行3个路径,根据爬行的路径长不小于15,不超过20,可得爬行的次数,根据爬行的次数,可得点的坐标;
根据先向右爬行2个单位长度,再向上爬行2个单位长度,可得每次爬行4个路径,根据爬行的路径长不小于15,不超过20,可得爬行的次数,根据爬行的次数,可得点的坐标.
解答 解:(1)当选择动作①爬行时,如图1 ,
,
当选择②爬行时,如图2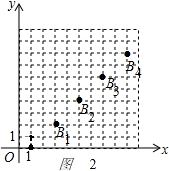 ,
,
(2)点A1,A2,A3,A4的坐标都满足关系式:x-2y=1,
点B1,B2,B3,B4的坐标满足关系式:x-y=1,
故答案为:1,x-y=1;
(3)①由先向右爬行2个单位长度,再向上爬行1个单位长度,得
每次爬行的路径是3.
由蜘蛛P从A点出发爬行的路径长不小于15,不超过20,得
需爬行5次或6次.
当爬行5次时,到达A5,横坐标是2×5+1=11,纵坐标是5,
即A5(11,5);
当爬行6次时,即到达A6,横坐标是2×6+1=13,纵坐标是6,
即A6(13,6);
综上所述:蜘蛛P从A点出发爬行的路径长不小于15,不超过20,蜘蛛按①种规定动作爬行分别到达的点的坐标A5(11,5),或A6(13,6);
②由先向右爬行2个单位长度,再向上爬行2个单位长度,得
每次爬行的路径是4.
由蜘蛛P从A点出发爬行的路径长不小于15,不超过20,得
需爬行4次或5次.
当爬行4次时,即到达B4,横坐标是2×4+1=9,纵坐标2×4=8,
即B4(9,8);
当需爬行5次时,即到达B5,横坐标是2×5+1=11,纵坐标是2×5=10,
即B5(11,10).
综上所述:蜘蛛P从A点出发爬行的路径长不小于15,不超过20,蜘蛛按②种规定动作爬行分别到达的点的坐标B4(9,8)或B5(11,10).
点评 本题考查了一次函数综合题,利用爬行规律得出每次爬行后横坐标与纵坐标的关系是解题关键,要分类讨论,以防遗漏.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
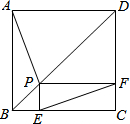 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列四个结论:
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
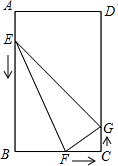 如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2.
如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
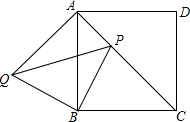 如图,在正方形ABCD中,点P是对角线AC上一点,把△BPC绕着点B逆时针旋转得到△BQA.
如图,在正方形ABCD中,点P是对角线AC上一点,把△BPC绕着点B逆时针旋转得到△BQA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日 6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2013年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图),同时将前4个月的用电量和相应电费制成表格(如表).根据上述信息,解答下列问题:
小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日 6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2013年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图),同时将前4个月的用电量和相应电费制成表格(如表).根据上述信息,解答下列问题:| 月用电量(度) | 电费(元) | |
| 1月 | 90 | 51.80 |
| 2月 | 92 | 50.85 |
| 3月 | 98 | 49.24 |
| 4月 | 105 | 48.55 |
| 5月 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的坐标分别为A(-1,0),B(-2,-1),C(-1,-2)
如图,△ABC的坐标分别为A(-1,0),B(-2,-1),C(-1,-2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com