
【题目】如图1,在平面直角坐标系中,已知A(a,b),且a.b满足![]() ,
,
(1)求A点的坐标及线段OA的长度;(2)点P为x轴正半轴上一点,且△AOP是等腰三角形,求P点的坐标;
(3)如图2,若B(1,0),C(0,-3),试确定∠ACO+∠BCO的值是否发生变化,若不变,求其值;若变化,请求出变化范围。


【答案】(1)![]() ;(2)P(
;(2)P(![]() ,0)或P(4,0)、P(
,0)或P(4,0)、P(![]() ,0);(3)45.
,0);(3)45.
【解析】
(1)先由二次根式有意义的条件得出a的值,再代入等式得出b的值,从而得出点A的坐标,继而利用两点间的距离公式可得OA的长;
(2)分OA=OP、AO=AP、PO=PA三种情况,利用等腰三角形的性质逐一求解可得;
(3)在x轴负半轴上取一点,使得OD=OB=1,知点B与点D关于y轴对称,据此得∠BCO=∠DCO,根据两点间的距离公式知AD2=10,CD2=10,AC2=20,依据勾股定理逆定理判断出△ACD是等腰直角三角形,利用∠ACO+∠BCO=∠ACO+∠DCO=∠ACD可得答案.
解:
(1)∵![]() ,
,
∴a=2,
则b=1,
∴A(2,1),
则OA=![]() =
=![]() ;
;
(2)当OA=OP时,P(![]() ,0);
,0);
当AO=AP时,如图1,作AH⊥x轴于点H,
则OH=PH=2,
∴OP=4,
∴P(4,0);
当P′O=P′A时,设P′O=P′A=x,则P′H=2-x,
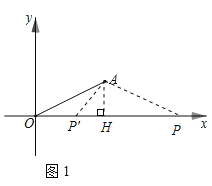
由AP′2=P′H2+AH2得(2-x)2+12=x2,
解得:x=![]() ,
,
∴P(![]() ,0).
,0).
(3)如图2,在x轴负半轴上取一点,使得OD=OB=1,
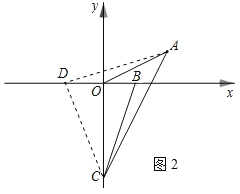
则点B与点D关于y轴对称,
∴∠BCO=∠DCO,
∵A(2,1),D(-1,0),C(0,-3),
∴AD2=32+12=10,CD2=12+32=10,AC2=22+42=20,
∴AD2+CD2=AC2,且AD=CD,
∴△ACD是等腰直角三角形,
则∠ACO+∠BCO=∠ACO+∠DCO=∠ACD=45°.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点D的坐标是(-3,1),点A的坐标是(4,3).

(1)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF,并直接写出E、F的坐标.
(2)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为多少?
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学组织春游活动,到超市选购A, B两种饮料,若购买6瓶A种饮料, 4瓶B种饮料需花费39元,购买20瓶A种饮料和30瓶B种饮料需花费180元。
(1)购买A, B两种饮料每瓶各多少元?
(2)实际购买时,恰好超市进行促销活动,如果一次性购买 A种饮料数量超过20瓶,则超出部分的价格享受八折优惠,B种饮料价格保持不变,若购买B种饮料的数量是A种饮料数量的2倍还多10瓶,且总费用不超过320元则最多可购买A种饮料多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数![]() (件)与价格
(件)与价格![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
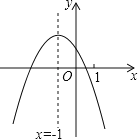
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(﹣1,0),C(﹣4,3).
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;(其中A1、B1、C1分别是A、B、C的对应点,不写画法.)
(2)写出点A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在相邻两点距离为1的点阵纸上(左右相邻或上下相邻的两点之间的距离都是1个单位长度),三个顶点都在点阵上的三角形叫做点阵三角形,请按要求完成下列操作:

(1)将点阵△ABC水平向右平移4个单位长度,再竖直向上平移5个单位长度,画出平移后的△A1B1C1;
(2)连接AA1、BB1,则线段AA1、BB1的位置关系为 、数量关系为 .估计线段AA1的长度大约在 <AA1< 单位长度:(填写两个相邻整数);
(3)画出△ABC边AB上的高CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com