
【题目】等腰三角形ABC中,AB=AC,D、E分别是AC、AB上两点,连结BD、CE,BD=CE,且BC>BD,∠A=48°,∠BCE=36°,则∠ADB的度数等于________.
【答案】102°
【解析】
作BG⊥AC于G,作CH⊥AB于H,则∠BHC=∠EHC=∠CGB=∠DGB=90°,由AAS证明△BCH≌△CBG,得出CH=BG,再由HL证明Rt△BDG≌Rt△CEH,得出∠BDG=∠CEH,得出∠ADB=∠AEC,由三角形外角性质求出∠AEC=∠ABC+∠BCE=102°,即可得出结果.
解:作BG⊥AC于点G,作CH⊥AB于点H,如图:
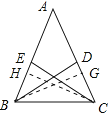
∴∠BHC=∠EHC=∠CGB=∠DGB=90°,
∵AB=AC, ∠A=48°,
∴∠ABC=∠ACB=![]() (180°-∠A)=66°,
(180°-∠A)=66°,
在△BCH和△CBG中,
∵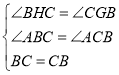 ,
,
∴△BCH≌△CBG(AAS),
∴CH=BG,
在Rt△BDG和Rt△CEH中,
∵![]() ,
,
∴Rt△BDG≌Rt△CEH(HL),
∴∠BDG=∠CEH,
∴∠ADB=∠AEC,
∵∠AEC=∠ABC+∠BCE=66°+36°=102°,
∴∠ADB=102°.
故答案为:102°.


科目:初中数学 来源: 题型:
【题目】如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE//OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2-12+36+|n-2m|=0.
(1)求A、B两点的坐标?
(2)若点D为AB中点,求OE的长?
(3)如图2,若点P(x,-2x+6)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2020分钟时,这个粒子所在位置的坐标是( )
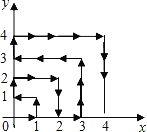
A.(4,45)B.(45,4)C.(44,4)D.(4,44)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为![]() 的正方形图形分割成四部分(两个正方形和两个长方形),请认真观察图形,解答下列问题:
的正方形图形分割成四部分(两个正方形和两个长方形),请认真观察图形,解答下列问题:
(1)根据图中条件,请用两种方法表示该图形的总面积(用含![]() 的代数式表示出来);
的代数式表示出来);
(2)如果图中的![]() 满足
满足![]() 求
求![]() 的值;
的值;
(3)已知![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
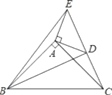
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,己知
中,己知![]() ,
,![]() ,将线段OA平移至CB,点D在
,将线段OA平移至CB,点D在![]() 轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
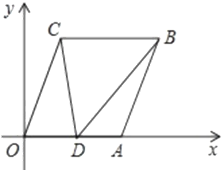
(1)直接写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的2倍时,求点D的坐标;
(3)若∠OCD=25°,∠DBA=15°,求∠BDC.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y1=x2﹣2x﹣3先向左平移1个单位,再向上平移4个单位后,与抛物线y2=ax2+bx+c重合,现有一直线y3=2x+3与抛物线y2=ax2+bx+c相交,当y2≤y3时,利用图象写出此时x的取值范围是( )
A. x≤﹣1 B. x≥3 C. ﹣1≤x≤3 D. x≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DF∥AB,DE∥BC,连接BD.
(1)求证:△DEB≌△BFD;
(2)若点D是AC边的中点,当△ABC满足条件_____时,四边形DEBF为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
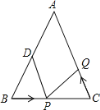
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为_____厘米/秒,△BPD与△CQP全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com