Question

学生节活动有一个抽奖节目，给每个游戏者一个均匀色子（正方体，六个面分别是1到6这六个数字），分别丢两次，则朝上一面的两个数字和如果大于或等于10，或者两数字和小于或等于3都算中奖．
问：（1）丢两次的数字之和共有多少种不同的和？分别是什么？
（2）中奖的概率为多少？

Answer 1

	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

解：以第一次丢出的数字为列，第二次丢出的数学为行，则两次丢出数学之和可表示为下面表格
（1）由表可知数字之和有：2，3，4，5，6，7，8，9，10，11，12共11种．
（2）中奖的情况：小于等于3的有三种，大于等于10的有6种共有9种中奖情况，总共有36种抽奖的结果，
所以中奖的概率为．
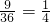
分析：（1）利用列表法，分别求出两次数字之和即可；
（2）根据列表可以得到共有36种结果，数出于等于10的有几种，根据概率公式即可求解．
点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．
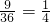