
����Ŀ��Rt��ABC�У���C=90�㣬��D��E�ֱ��DZ�AC��BC�ϵĵ㣬��P��һ���㣮���PDA=��1����PEB=��2����DPE=�Ϧ���
��1������P���߶�AB�ϣ���ͼ�٣��ҡϦ�=50�㣬���1+��2=�� 
��2������P��б��AB���˶�����ͼ�ڣ���Ϧ�����1����2֮��Ĺ�ϵΪ�� 
��3����ͼ�ۣ�����P��б��BA���ӳ������˶���CE��CD������ֱ��д���Ϧ�����1����2֮��Ĺ�ϵ���� 
��4������P�˶�����ABC���⣨ֻ���о�ͼ�����Σ�����Ϧ�����1����2֮���кι�ϵ����˵�����ɣ� 
���𰸡�
��1��140��
��2���⣺��1+��2=90��+�Ϧ�
��3���⣺��2����1=90��+�Ϧ�����2=��1+90�㣻��1����2=�Ϧ���90��
��4���⣺

�ߡ�PFD=��EFC��
��180�㩁��PFD=180�㩁��EFC��
��Ϧ�+180�㩁��1=��C+180�㩁��2��
���2=90��+��1������
�ʴ�Ϊ����2=90��+��1����
���������⣺��1����ͼ������PC�� �ߡ�1=��PCD+��CPD����2=��PCE+��CPE��
���1+��2=��PCD+��CPD+��PCE+��CPE=��DPE+��C��
�ߡ�DPE=�Ϧ�=50�㣬��C=90�㣬
���1+��2=50��+90��=140�㣬
���Դ��ǣ�140�㣻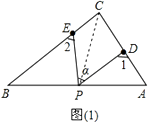
����2������PC��
�ߡ�1=��PCD+��CPD����2=��PCE+��CPE��
���1+��2=��PCD+��CPD+��PCE+��CPE=��DPE+��C��
�ߡ�C=90�㣬��DPE=�Ϧ���
���1+��2=90��+�Ϧ���
���Դ��ǣ���1+��2=90��+�Ϧ���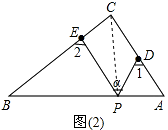
����3����ͼ1��
�ߡ�2=��C+��1+�Ϧ���
���2����1=90��+�Ϧ���
��ͼ2���Ϧ�=0�㣬��2=��1+90�㣻
��ͼ3���ߡ�2=��1���Ϧ�+��C��
���1����2=�Ϧ���90�㣮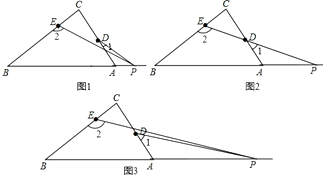
���Դ��ǣ���2����1=90��+�Ϧ�����2=��1+90�㣻��1����2=�Ϧ���90�㣮
�����㾫����������Ĺؼ��������������ε��ڽǺ���ǵ����֪ʶ�����������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ��Լ��������ε���ǵ����⣬�˽�������һ������һ�ߵ��ӳ�����ɵĽǣ��������ε���ǣ������ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�Ƶ�O����ʱ�뷽����ת���ı���A��B��C��D��,���ı���A��B��C��D����__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬AC=60cm����A=60�㣬��D�ӵ�C������CA������4cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루0��t��15��������D��DF��BC�ڵ�F������DE��EF��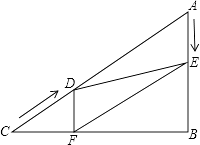
��1����֤��AE=DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ�˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=AC��AD��BC������Ϊ��D��AN�ǡ�ABC��ǡ�CAM��ƽ���ߣ�CE��AN������Ϊ��E�� 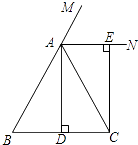
��1����֤���ı���ADCEΪ���Σ�
��2������ABC����ʲô����ʱ���ı���ADCE��һ�������Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����õ��ԣ���ͬһҳ���ijͼ�ν��и��ƣ��õ�һ��ͼ������һ��ͼ�����Կ���һ������ͼ��ͨ���� ���õ���
A. ��ת B. ƽ�ƺ���ת
C. ƽ�� D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A����ζ���ʽ��B�����ζ���ʽ����A+Bһ���ǣ� ��
A.��ζ���ʽ
B.�˴ζ���ʽ
C.���ζ���ʽ
D.��������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() ��
��![]() �ύ�ڵ�A��4��0������
�ύ�ڵ�A��4��0������![]() �ύ�ڵ�B����x������һ����E��m��0����0��m��4��������E��
�ύ�ڵ�B����x������һ����E��m��0����0��m��4��������E��![]() ��Ĵ��߽�ֱ��AB�ڵ�N�����������ڵ�P������P��PM��AB�ڵ�M��
��Ĵ��߽�ֱ��AB�ڵ�N�����������ڵ�P������P��PM��AB�ڵ�M��
��1����![]() ��ֵ��ֱ��AB�ĺ�������ʽ��
��ֵ��ֱ��AB�ĺ�������ʽ��
��2����P���˶��Ĺ����У����ú�m�Ĵ���ʽ��ʾ�߶�PN��
��3������PMN���ܳ�Ϊ![]() ����AEN���ܳ�Ϊ
����AEN���ܳ�Ϊ![]() ����
����![]() ����m��ֵ��
����m��ֵ��
��4����ͼ2���ڣ�3�������£����߶�OE�Ƶ�O��ʱ����ת�õ�OE������ת��Ϊ����0��������90����������![]() ��
��![]() ����
����![]() ����Сֵ��
����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ��������֮��ͬ��С�ij��˵��⣬�������ĸ���������AB=BC���ڡ�ABC=90�㣬��AC=BD����AC��BD��ѡ������Ϊ����������ʹABCDΪ�����Σ���ͼ����������������ѡ��������Ϊ���д�����ǣ� �� 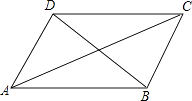
A.�٢�
B.�ڢ�
C.�٢�
D.�ڢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com