

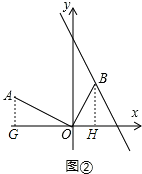
| AG |
| OH |
| GO |
| BH |
| 1 |
| x |
| 2 |
| -2x+3 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
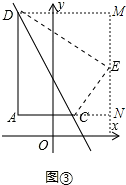
| DM |
| EN |
| ME |
| CN |
| DE |
| CE |
|
|
| 14 |
| 5 |
| 17 |
| 5 |


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源:不详 题型:解答题
 同路线从广安赶往重灾区平武救援,下图表示其行驶过程中路程随时间的变化图象.
同路线从广安赶往重灾区平武救援,下图表示其行驶过程中路程随时间的变化图象.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 4 |
| 3 |
 个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.
个根,OB=BC,D、E分别是线段OC、OB上的动点(点D与点O、点C不重合),且∠BDE=∠ABO,设CD=x,BE=y.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.9cm | B.10cm | C.10.5cm | D.11cm |

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com