
| A. | 0或3 | B. | 0或-3 | C. | -3 | D. | 3 |
分析 根据反比例函数系数k=xy,得到k=mn=(n+1)(m-1),从而求得m-n=1,k=(m2-1)(n2-1)变形为k=k(mn-2),即可求得mn=3.
解答 解:∵双曲线y=$\frac{k}{x}$经过点(m,n),(n+1,m-1),(m2-1,n2-1),
∴k=mn=(n+1)(m-1)
∴mn=mn+m-n-1,
∴m-n=1,
∴k=(m2-1)(n2-1)=(m+1)(m-1)(n+1)(n-1)=k(m+1)(n-1)=k(mn-m+n-1)=k(mn-1-1)=mn(mn-2)=k(mn-2),
∴mn-2=1,
∴k=mn=3,
故选D.
点评 本题考查了反比例函数图象上点坐标特征,反比例函数y=$\frac{k}{x}$中,k=xy上解题点关键.


科目:初中数学 来源: 题型:解答题
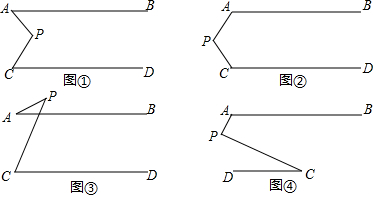
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
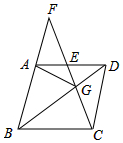 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
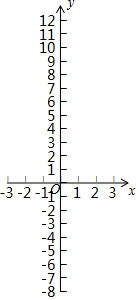 佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.| x | … | -3 | -$\frac{5}{2}$ | -2 | -$\frac{3}{2}$ | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | … |
| y | … | -8 | -$\frac{21}{8}$ | 0 | $\frac{5}{8}$ | m | -$\frac{9}{8}$ | -2 | -$\frac{15}{8}$ | 0 | $\frac{35}{8}$ | 12 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 104倍 | B. | 106倍 | C. | 108倍 | D. | 1010倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
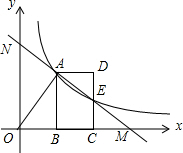 如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com