
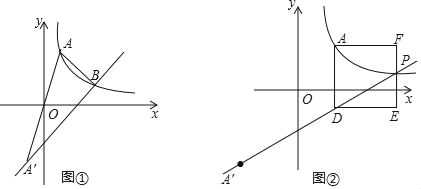
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
【答案】(1)y1=![]() ,y2=x﹣2;②2<x<4;(2)k=6;(3)证明见解析.
,y2=x﹣2;②2<x<4;(2)k=6;(3)证明见解析.
【解析】(1)由已知代入点坐标即可;
(2)面积问题可以转化为△AOB面积,用a、k表示面积问题可解;
(3)设出点A、A′坐标,依次表示AD、AF及点P坐标.
(1)①由已知,点B(4,2)在y1═![]() (x>0)的图象上
(x>0)的图象上
∴k=8
∴y1=![]()
∵a=2
∴点A坐标为(2,4),A′坐标为(﹣2,﹣4)
把B(4,2),A(﹣2,﹣4)代入y2=mx+n得,
![]() ,
,
解得![]() ,
,
∴y2=x﹣2;
②当y1>y2>0时,y1=![]() 图象在y2=x﹣2图象上方,且两函数图象在x轴上方,
图象在y2=x﹣2图象上方,且两函数图象在x轴上方,
∴由图象得:2<x<4;
(2)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO,
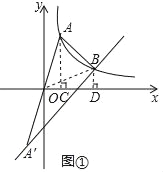
∵O为AA′中点,
S△AOB=![]() S△AOA′=8
S△AOA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,![]() )(3a,
)(3a,![]() )
)
∴![]() ,
,
解得k=6;
(3)由已知A(a,![]() ),则A′为(﹣a,﹣
),则A′为(﹣a,﹣![]() ).
).
把A′代入到y=![]() ,得:﹣
,得:﹣![]() ,
,
∴n=![]() ,
,
∴A′B解析式为y=﹣![]() .
.
当x=a时,点D纵坐标为![]() ,
,
∴AD=![]()
∵AD=AF,
∴点F和点P横坐标为![]() ,
,
∴点P纵坐标为![]() .
.
∴点P在y1═![]() (x>0)的图象上.
(x>0)的图象上.


科目:初中数学 来源: 题型:
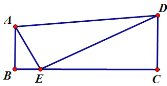
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED=90°
(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE
(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
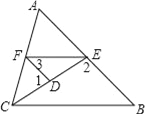
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P、Q同时停止运动,若点P与点Q的速度之比为1:2,则下列说法正确的是( )
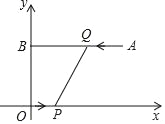
A. 线段PQ始终经过点(2,3)
B. 线段PQ始终经过点(3,2)
C. 线段PQ始终经过点(2,2)
D. 线段PQ不可能始终经过某一定点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(m,2)在直线![]() :y=2x上,过点A的直线
:y=2x上,过点A的直线![]() 与x轴交于点B(4,0).
与x轴交于点B(4,0).
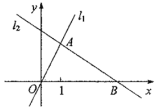
(1)求直线![]() 的解析式;
的解析式;
(2)己知点P.的坐标为(n,0),过点P垂直x轴的直线与![]() ,
,![]() 分别交于点C,D,当点C位于点D上方时,求n的取值范围.
分别交于点C,D,当点C位于点D上方时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索发现)有绝对值的定义可得,数轴上表示数![]() 的点到原点的距离为
的点到原点的距离为![]() .小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为
.小丽进一步探究发现,在数轴上,表示3和5的两点之间的距离为![]() ;表示
;表示![]() 和5的两点之间的距离为
和5的两点之间的距离为![]() ;表示
;表示![]() 和
和![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(概括总结)根据以上过程可以得出:数轴上,表示数![]() 和数
和数![]() 的两点之间的距离为
的两点之间的距离为![]() .
.
(问题解决)
(1)若![]() ,则
,则![]() ________;
________;
(2)若![]() ,则
,则![]() ________;
________;
(3)若![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
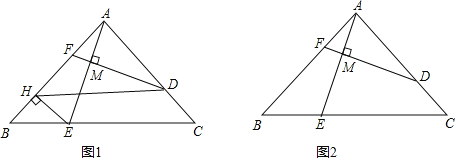
【题目】已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且![]() =
=![]() =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
=m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
(1)如图1,过点E作EH⊥AB于点H,连结DH.
①求证:四边形DHEC是平行四边形;
②若m=![]() ,求证:AE=DF;
,求证:AE=DF;
(2)如图2,若m=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】来自某综合市场财务部的报告表明,商场2014年1﹣4月份的投资总额一共是2065万元,商场2014年第一季度每月利润统计图和2014年1﹣4月份利润率统计图如下(利润率=利润÷投资金额).则商场2014年4月份利润是__万元.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com