
【题目】小明从如图所示的二次函数![]() 的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④
的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④![]() >4ac,⑤2a=-2b,其中正确结论是( ).
>4ac,⑤2a=-2b,其中正确结论是( ).
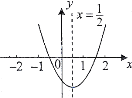
A.①②④B.②③④C.③④⑤D.①③⑤
【答案】C
【解析】
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
①由抛物线交y轴于负半轴,则c<0,故①错误;
②由抛物线的开口方向向上可推出a>0;
∵对称轴在y轴右侧,对称轴为x=![]() >0,
>0,
又∵a>0,
∴b<0;
由抛物线与y轴的交点在y轴的负半轴上,
∴c<0,
故abc>0,故②错误;
③结合图象得出x=1时,对应y的值在x轴上方,故y>0,即ab+c>0,故③正确;
④由抛物线与x轴有两个交点可以推出b24ac>0,故④正确;
⑤由图象可知:对称轴为x=![]() =
=![]()
则2a=2b,故⑤正确;
故正确的有:③④⑤.
故选:C


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一次防流感知识检测中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次检测中甲、乙两组学生人数相同,成绩如下两个统计图:
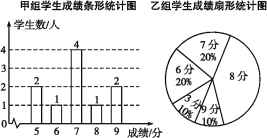
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请列式计算乙组平均分,补充完整下面的成绩统计分析表所有空格:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 2.6 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
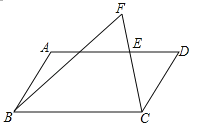
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
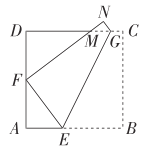
【题目】如图,在正方形ABCD中,DC=8,现将四边形BEGC沿折痕EG(G,E分别在DC,AB边上)折叠,其顶点B,C分别落在边AD上和边DC的上部,其对应点设为F,N点,且FN交DC于M.
特例体验:
(1)当FD=AF时,△FDM的周长是多少?
类比探究:
(2)当FD≠AF≠0时,△FDM的周长会发生变化吗?请证明你的猜想.
拓展延伸:
(3)同样在FD≠AF≠0的条件下,设AF为x,被折起部分(即:四边形FEGN)的面积为S,试用含x的代数式表示S,并问:当x为何值时,S=26?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市场将进货价为40元/件的商品按60元/件售出,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元/件,每星期该商品要少卖出10件.
(1)请写出该商场每月卖出该商品所获得的利润y(元)与该商品每件涨价x(元)间的函数关系式;
(2)每月该商场销售该种商品获利能否达到6300元?请说明理由;
(3)请分析并回答每件售价在什么范围内,该商场获得的月利润不低于6160元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
科目:初中数学 来源: 题型:
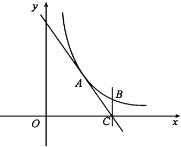
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(1)求k的值与B点的坐标;
(2)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,试写出符合条件的所有D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com