
【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过![]() 方时,每方的收费标准为
方时,每方的收费标准为![]() 元,当用水量超过
元,当用水量超过![]() 方时,超出
方时,超出![]() 方的部分每方的收费标准为
方的部分每方的收费标准为![]() 元,下表是小明家
元,下表是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
用水量(方) |
|
|
|
|
费用(元) |
|
|
|
|
请根据表格中提供的信息,回答以下问题:
(1)![]() ___________.
___________.![]() ____________;
____________;
(2)若小明家![]() 月份交纳水费
月份交纳水费![]() 元,则小明家
元,则小明家![]() 月份用水多少方?
月份用水多少方?
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的某圆上,有弦MN,取MN的中点P,我们规定:点P到某点(直线)的距离叫做“弦中距”,用符号“![]() ”表示.
”表示.
现请在以W(-3,0)为圆心,半径为2的⊙W圆上,根据以下条件解答所提问题:
(1)已知弦MN长度为2.
①如图1:当MN∥x轴时,直接写出到原点O的![]() 的长度;
的长度;
②如果MN在圆上运动时,在图2中画出示意图,并直接写出到点O的![]() 的取值范围.
的取值范围.
(2)已知点![]() ,点N为⊙W上的一动点,有直线
,点N为⊙W上的一动点,有直线![]() ,求到直线
,求到直线![]() 的
的![]() 的最大值.
的最大值.
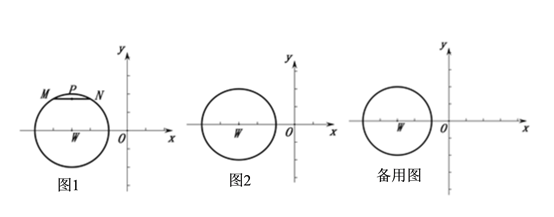
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解该市九年级学生上学期参加综合实践活动的情况,随机调查了该市光明中学九年级学生上学期参加综合实践活动的时间,并用得到的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,回答下列问题:
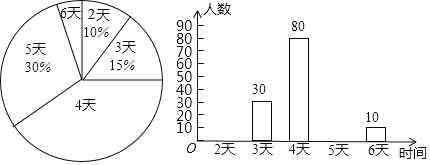
(1)试求出该校九年级学生总数;
(2)分别求出活动时间为2天、5天的学生人数,并补全条形统计图;
(3)如果该市九年级学生共约50000人,请你估计“活动时间不少于4天”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和不小于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级二班的几位同学正在一起讨论一个关于数轴上的点表示数的题目:
甲说:“这条数轴上的两个点![]() 、
、![]() 表示的数都是绝对值是4的数”;
表示的数都是绝对值是4的数”;
乙说:“点![]() 表示负整数,点
表示负整数,点![]() 表示正整数,且这两个数的差是3”;
表示正整数,且这两个数的差是3”;
丙说:“点![]() 表示的数的相反数是它本身”.
表示的数的相反数是它本身”.
(1)请你根据以上三位同学的发言,画出一条数轴,并描出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个不同的点.
五个不同的点.
(2)求这个五个点表示的数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某小学“演讲大赛”选拔赛初赛中,甲、乙、丙三位评委对小选手的综合表现,分别给出“待定”(用字母W表示)或“通过”(用字母P表示)的结论.
⑴请用树状图表示出三位评委给小选手琪琪的所有可能的结论;
⑵对于小选手琪琪,只有甲、乙两位评委给出相同结论的概率是多少?
⑶比赛规定,三位评委中至少有两位给出“通过”的结论,则小选手可入围进入复赛,问琪琪进入复赛的概率是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
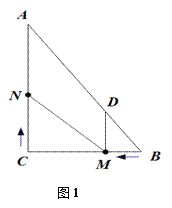
【题目】如图1,在Rt△ABC中,∠C=90,BC=6,AC=8.动点M从点B开始沿边BC向点C以每秒1个单位长度的速度运动,动点N从点C开始沿边CA向点A以每秒2个单位长度的速度运动,点M、N同时出发,且当其中一点到达端点时,另一点也随之停止运动.过点M作MD∥AC,交AB于点D,连接MN.设运动时间为t秒(t≥0).
(1)当t为何值时,四边形ADMN为平行四边形?
(2)是否存在t的值,使四边形ADMN为菱形?若存在,求出t的值;若不存在,说明理由.并探究只改变点N的速度(匀速运动),使四边形ADMN在某一时刻为菱形,求点N的速度;
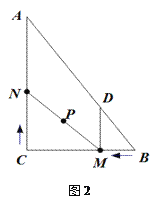
(3)如图2,在整个运动过程中,求出线段MN中点P所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com