
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
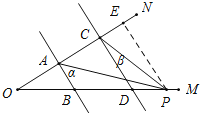
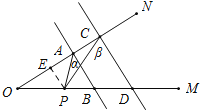
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

【答案】(1)110°.(2)∠APC=∠α+∠β,(3)当P在BD延长线上时,∠CPA=∠α﹣∠β;当P在DB延长线上时,∠CPA=∠β﹣∠α.
【解析】
试题(1)过点P作PE∥AB,则有PE∥AB∥CD,根据两直线平行,同旁内角互补得到∠A+∠APE=180°,∠C+∠CPE=180°,再根据∠APC=∠APE+∠CPE和已知∠APE和∠CPE度数即可求出∠APC的角度。(2)过P作PE∥AB交AC于E,则有AB∥PE∥CD,进而得到∠α=∠APE,∠β=∠CPE,再根据∠APC=∠APE+∠CPE,即可用α、β来表示∠APC的度数;(3)根据题意画出图形,当P在BD延长线上时,P作PE∥AB交AC于E,则有AB∥PE∥CD,可得到∠CPA=∠β﹣∠α,当如图所示,当P在DB延长线上时,P作PE∥AB交AC于E,则有AB∥PE∥CD,可得到∠CPA=∠β﹣∠α;
试题解析:
(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
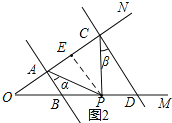
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.
计算:(1)i.i2.i3.i4
(2)i+i2+i3+i4+…+i2017+i2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )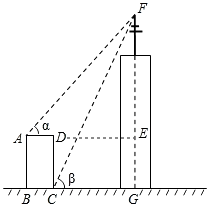
A.(35 ![]() +55)m
+55)m
B.(25 ![]() +45)m
+45)m
C.(25 ![]() +75)m
+75)m
D.(50+20 ![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
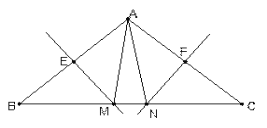
【题目】如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =10cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
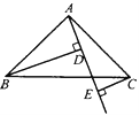
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:
(1)AD与CE的大小关系如何?请说明理由;
(2)若BD=5,CE=2,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com