练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
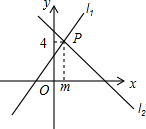
    1．如图l1：y=x+3与l2：y=ax+b相交于点P（m，4），则关于x的不等式x+3≤ax+b的解为（　　）
    A．x≥4B．x＜mC．x≥mD．x≤1

    分析 首先把P（m，4）代入y=x+3可得m的值，进而得到P点坐标，然后再利用图象写出不等式的解集即可．

    解答 解：把P（m，4）代入y=x+3得：m=1，
    则P（1，4），
    根据图象可得不等式x+3≤ax+b的解集是x≤1，
    故选D．

    点评 本题主要考查一次函数和一元一次不等式，本题是借助一次函数的图象解一元一次不等式，两个图象的“交点”是两个函数值大小关系的“分界点”，在“分界点”处函数值的大小发生了改变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

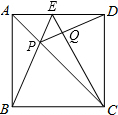    11．如图，已知正方形ABCD，E为AD的中点，连接BE和EC，BE交AC于点P，连接DP，交CE于Q．求证：
    （1）△ABP≌△ADP；
    （2）DP⊥CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．（1）计算：2$\sqrt{18}+6\sqrt{\frac{1}{2}}-3\sqrt{32}$；
    （2）已知：x=2-$\sqrt{3}$，求代数式（7+4$\sqrt{3}$）x2-（2+$\sqrt{3}$）x-$\sqrt{3}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．若关于x的一元二次方程x2+2（m-2）x+m2=0没有实数根，则m的取值范围是（　　）
    A．m＞1B．m≥1C．m＜1D．m≤1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

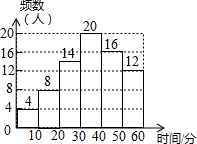    16．小文同学统计了他所在小区居民每天微信阅读的时间，并绘制了直方图．
    ①小文同学一共统计了60人
    ②每天微信阅读不足20分钟的人数有8人
    ③每天微信阅读30-40分钟的人数最多
    ④每天微信阅读0-10分钟的人数最少
    根据图中信息，上述说法中正确的是（　　）
    A．①②③④B．①②③C．②③④D．③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．定义：对于线段MN和点P，当PM=PN，且∠MPN≤120°时，称点P为线段MN的“等距点”．特别地，当PM=PN，且∠MPN=120°时，称点P为线段MN的“强等距点”．如图1，在平面直角坐标系xOy中，点A的坐标为$（2\sqrt{3}，0）$．

    （1）若点B是线段OA的“强等距点”，且在第一象限，则点B的坐标为（$\sqrt{3}$，1）；
    （2）若点C是线段OA的“等距点”，则点C的纵坐标t的取值范围是t≥1或t≤-1；
    （3）将射线OA绕点O顺时针旋转30°得到射线l，如图2所示．已知点D在射线l上，点E在第四象限内，且点E既是线段OA的“等距点”，又是线段OD的“强等距点”，求点D坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．规定：[x]表示不超过x的最大整数，例如：[3.69]=3，[-3.69]=-4，$[\sqrt{3}]=1$．计算：$[\sqrt{13}]-1$=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．一个三角形的两边长分别为2和6，则第三边的长可能为（　　）
    A．4B．7C．8D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，△ABC为边长是4$\sqrt{3}$的等边三角形，四边形DEFG是边长是6的正方形．现将等边△ABC和正方形DEFG按如图①的方式摆放，使点C与点E重合，点B、C、E、F在同一条直线上，△ABC从图①的位置出发，以每秒1个单位长度的速度沿EF方向向右匀速运动，当点B与点E重合时停止运动，设△ABC的运动时间为t秒．
    （1）当点A与点D重合时，求此时t的值；
    （2）在整个运动过程中，设等边△ABC和正方形DEFG重叠部分的面积为S，求S与t之间的函数关系式；
    （3）如图②，当点A与点D重合时，作∠ABE的角平分线BM交AE于点M，将△ABM绕点A逆时针旋转，使边AB与边AC重合，得到△ACN．在线段AG上是否存在H点，使得△ANH为等腰三角形？若存在，求线段AH的长度；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案