Question

已知圆O的直径AB=2cm，过A点的两弦AC=

2

cm，AD=

3

cm，则∠CAD所夹圆内部分的面积是

 

cm²．

Answer 1

分析：先根据题意画出图形，由于不明确AC、AD的位置关系，故应分两种情况讨论：
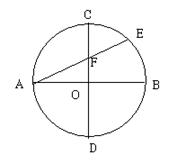
（1）如图（1），当AC、AD在直径AB的同侧时，连接BC、BD、OC、OD分别根据三角形的直径及弦长求出∠1、∠2的度数，进而求出扇形BOD及BOC的面积，过O作OF⊥AD于F，再求出△AOC及△AOD的面积，再求出三角形及扇形的面积和即可．
（2）同（1）作出辅助线，求出扇形BOD及BOC的面积，△AOC及△AOD的面积，再求出三角形及扇形的面积和即可．∠CAD所夹圆内部分的面积=S_扇形BOC+S_△AOC-S_扇形BOD-S_△AOD．

解答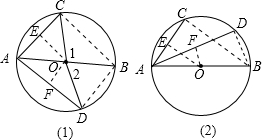：解：（1）如图（1），连接BC、BD、OC、OD，
∵AB是⊙O的直径，∴∠ACB=∠ADB=90°，
∵OC=OA=

1

2

AB=

1

2

×2=1，AC=

2

cm，
∴1²+1²=（

2

）²，即OA²+OC²=（AC）²，
∴△AOC是等腰直角三角形，∴S_△AOC=

1

2

×1×1=

1

2

；
∴∠BOC=90°，S_扇形BOC=

90°π×12

360°

=

π

4

；
在△AOD中，过O作OF⊥AD于F，
∵OA=OD=1，∴AF=DF=

1

2

AD=

1

2

×

3

=

3

2

．
OF=

OA2-AF2

=

12-( 3 2 )2

=

1

2

，
∴S_△AOD=

1

2

×AD×OF=

1

2

×

3

×

1

2

=

3

4

．
在Rt△AOD中，BD=

AB2-AD2

=

22- 3 2

=1，
∴△BOD是等边三角形，∠BOD=60°，
∴S_扇形BOD=

60π×12

360

=

π

6

．
∴∠CAD所夹圆内部分的面积=S_△AOC+S_扇形BOC+S_△AOD+S_△AOD=

1

2

+

π

4

+

3

4

+

π

6

=

2+ 3

4

+

5π

12

（m²）．

（2）同（1），
∠CAD所夹圆内部分的面积=S_△AOC+S_扇形BOC-S_△AOD-S_△AOD=

1

2

+

π

4

-

3

4

-

π

6

=

2- 3

4

+

π

12

（m²）．

点评：此题比较复杂，解答此题的关键是作出辅助线，分别求出三角形及扇形的面积再解答．