Question

18．如图，已知抛物线y=-$\frac{3}{16}$x²+bx+c与x轴，y轴分别交于A（12，0），B（0，9）两点，连接AB，射线AC平分∠BAO交y轴于点C，过点B作BP平行于AC交抛物线于点P；
（1）求抛物线的解析式；
（2）求直线AC的解析式；
（3）连接AP，试求四边形ACBP的面积；
（4）若有一动点Q以每秒1个单位的速度从A点开始沿射线AC移动，运动时间为t秒．在点Q的运动过程中，请直接写出t为何值时△OQA是等腰三角形．

Answer 1

分析 （1）把点A（12，0），B（0，9）代入抛物线的解析式求出b、c的值即可；
（2）AC平分∠BAO可知点C到AB、AO的距离相等，故可得出C点坐标，利用待定系数法求出直线AC的解析式即可；
（3）分AP=AO，AP=PO与AO=PO三种情况进行讨论即可．

解答 解：（1）∵抛物线y=-$\frac{3}{16}$x²+bx+c过A（12，0），B（0，9）两点，
∴$\left\{\begin{array}{l}-\frac{3}{16}×144+12b+c=0\\ c=9\end{array}\right.$，
解得$\left\{\begin{array}{l}b=\frac{3}{2}\\ c=9\end{array}\right.$．
∴抛物线的解析式为y=-$\frac{3}{16}$x²+$\frac{3}{2}$x+9；

（2）∵AC平分∠BAO，
∴点C到AB、AO的距离相等，
∴$\frac{{S}_{△ACO}}{{S}_{△ACB}}$=$\frac{AO}{AB}$=$\frac{12}{15}$=$\frac{4}{5}$．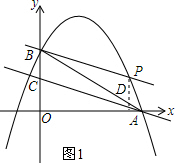
又∵$\frac{{S}_{△ACO}}{{S}_{△ACB}}$=$\frac{\frac{1}{2}CO•AO}{\frac{1}{2}BC•AO}$，
∴$\frac{CO}{BC}$=$\frac{4}{5}$．
∵CO=9，
∴C（0，4）；      
不妨设AC为y=kx+b，
∵A（12，0），C（0，4），
∴$\left\{\begin{array}{l}12k+b=0\\ b=4\end{array}\right.$，
解得$\left\{\begin{array}{l}k=-\frac{1}{3}\\ b=4\end{array}\right.$．
∴直线AC的解析式为y=-$\frac{1}{3}$x+4．

（3）∵BP∥AC，B（0，9），
∴直线BP的解析式为y=-$\frac{1}{3}$x+9，
∴$\left\{\begin{array}{l}y=-\frac{3}{16}{x}^{2}+\frac{3}{2}x+9\\ y=-\frac{1}{3}x+9\end{array}\right.$，
解得$\left\{\begin{array}{l}x=\frac{88}{9}\\ y=\frac{155}{27}\end{array}\right.$，
∴P（$\frac{88}{9}$，$\frac{155}{27}$）．
过点P作轴的y轴平行线交AB于点D（$\frac{88}{9}$，$\frac{5}{3}$），
∴S_△ABP=$\frac{1}{2}$（$\frac{155}{27}$-$\frac{5}{3}$）×12=$\frac{220}{9}$，
∴S_{四边形ACBP}=S_△ABP+S_△ABC=$\frac{220}{9}$+$\frac{1}{2}$×5×12=$\frac{490}{9}$．

（4）当AP=AO时，
∵A（12，0），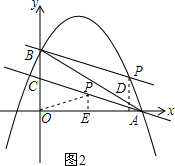
∴t=12（s）；
如图2，当AP=PO时，作OA的垂直平分线PE，
∵OA=12，
∴AE=6，
∴P（6，2），
∴AP=2$\sqrt{10}$，
∴t=2$\sqrt{10}$（s），
如图3，当AO=QO时，过点O作OE⊥AQ于点E，
∵A（12，0），C（0，4），
∴AC=$\sqrt{{12}^{2}+{4}^{2}}$=4$\sqrt{10}$，
∴OE=$\frac{4×12}{4\sqrt{10}}$=$\frac{6\sqrt{10}}{5}$，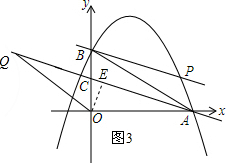
∴AE=$\sqrt{{12}^{2}-（\frac{6\sqrt{10}}{5}）^{2}}$=18$\sqrt{2}$，
∴AQ=36$\sqrt{2}$，
∴t=36$\sqrt{2}$（s）．
综上所述，当点t=12s，2$\sqrt{10}$s及36$\sqrt{2}$s时，△OQA是等腰三角形．

点评 本题考查的是二次函数综合题，涉及到利用待定系数法求二次函数的解析式、等腰三角形的判定与性质等知识，在解答（3）时要注意进行分类讨论．