
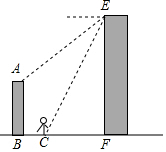
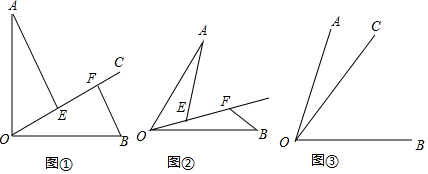
 为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工在塔EF的顶部处测得对面一栋AB=9米高的楼房顶部A的俯角为45°,测得楼房正前方BC=7米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?($\sqrt{3}$≈1.732,结果保留到1米.)
为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工在塔EF的顶部处测得对面一栋AB=9米高的楼房顶部A的俯角为45°,测得楼房正前方BC=7米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?($\sqrt{3}$≈1.732,结果保留到1米.) 分析 作AD⊥EF于D,根据题意得出DF=AB=9米,BC=7米,AD=BF,∠DAE=45°,∠FCE=60°,设CF=x米,解直角三角形得出FE=$\sqrt{3}$CF=$\sqrt{3}$x(米),AD=DE,因此DE=EF-FD=$\sqrt{3}$x-9(米),得出方程,解方程7+x=$\sqrt{3}$x-9即可求出CF,得出FE,即可得出结果.
解答 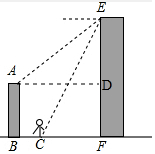 解:如图所示作AD⊥EF于D,
解:如图所示作AD⊥EF于D,
根据题意得:DF=AB=9米,BC=7米,AD=BF,∠DAE=45°,∠FCE=60°,
设CF=x米,
∵∠EFC=90°,∠FCE=60°,
∴FE=$\sqrt{3}$CF=$\sqrt{3}$x(米),
∴DE=EF-FD=$\sqrt{3}$x-9(米),
∵∠ADE=90°,∠DAE=45°,
∴AD=DE,
即7+x=$\sqrt{3}$x-9,
解得:x=8($\sqrt{3}$+1)米,
∴EF=$\sqrt{3}$x≈29(米),
答:塔的高度约为29米.
点评 本题考查解直角三角形的应用-仰角俯角问题,要求学生能借助仰角俯角构造直角三角形并解直角三角形,根据题意得出方程是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,交y轴于点D(0,-2),△AOB的面积为4
如图,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,交y轴于点D(0,-2),△AOB的面积为4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
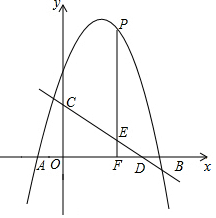 如图,抛物线y=-x2+4x+5与x轴交于A,B两点(点A在点B的左侧),直线y=$-\frac{3}{4}x+3$与y轴交于点C,与x轴交于点D.P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
如图,抛物线y=-x2+4x+5与x轴交于A,B两点(点A在点B的左侧),直线y=$-\frac{3}{4}x+3$与y轴交于点C,与x轴交于点D.P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com