
 人工浮床又称人工浮岛,自20年前人类开发出第一个人工浮床之后,就将人工浮床应用于地表水体的污染治理和生态修复.近年来,我国的人工浮床技术开发及用于正好处于快速发展时期.如图所示,是我市在某湖面上为净化水质而搭建的一个水上圆形人工浮床示意图,其中圆和三块边长为16米的正方形是浮岛框架部分,被分割成的7部分将运用无土技术分别栽培7种不同的水生植物,正方形的顶点A、B、C、D都在圆上,且整个浮床成轴对称图形,求这个圆形人工浮床的半径.
人工浮床又称人工浮岛,自20年前人类开发出第一个人工浮床之后,就将人工浮床应用于地表水体的污染治理和生态修复.近年来,我国的人工浮床技术开发及用于正好处于快速发展时期.如图所示,是我市在某湖面上为净化水质而搭建的一个水上圆形人工浮床示意图,其中圆和三块边长为16米的正方形是浮岛框架部分,被分割成的7部分将运用无土技术分别栽培7种不同的水生植物,正方形的顶点A、B、C、D都在圆上,且整个浮床成轴对称图形,求这个圆形人工浮床的半径. 分析 连接BD交EF于P,过P作PO⊥BD交HG于O,连接OB,根据全等三角形的性质得到PB=PE,由垂径定理得到点O为圆心,根据勾股定理得到BD=$\sqrt{3{2}^{2}+2{4}^{2}}$=40,得到PB=20,得到PH=4,根据相似三角形的性质得到HO=3,根据勾股定理即可得到结论.
解答 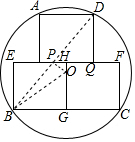 解:连接BD交EF于P,过P作PO⊥BD交HG于O,连接OB,
解:连接BD交EF于P,过P作PO⊥BD交HG于O,连接OB,
在△BEP与△PDQ中,$\left\{\begin{array}{l}{∠E=∠DQP}\\{∠EPB=∠EPQ}\\{BE=EQ}\end{array}\right.$,
∴△BEP≌△DQP,
∴PB=PD,
∴点O为圆心,
∵BD=$\sqrt{3{2}^{2}+2{4}^{2}}$=40,
∴PB=20,
∴PE=$\sqrt{P{B}^{2}-B{E}^{2}}$=12,
∴PH=4,
∵∠E=∠EHG=90°,
∴∠EBP+∠EPB=∠EPB+∠HPO=90°,
∴∠EPB=∠HPO,
∴△PBE∽△POH,
∴$\frac{PH}{BE}=\frac{HO}{PE}$,
∴HO=3,
∴OG=13,
∴OB=$\sqrt{B{G}^{2}+O{G}^{2}}$=5$\sqrt{17}$,
∴这个圆形人工浮床的半径为5$\sqrt{17}$米.
点评 本题考查了全等三角形的判断和性质,垂径定理的应用,轴对称图形的性质,相似三角形的判定和性质,正方形的性质,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )
在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=$\frac{m}{v}$,它的图象如图所示,则该气体的质量m为( )| A. | 1.4kg | B. | 5kg | C. | 7kg | D. | 6.4kg |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市重庆路水果市场某水果店购进甲、乙两种水果.已知1千克甲种水果的进价比1千克乙种水果的进价多4元,购进2千克甲种水果与1千克乙种水果共需20元.
我市重庆路水果市场某水果店购进甲、乙两种水果.已知1千克甲种水果的进价比1千克乙种水果的进价多4元,购进2千克甲种水果与1千克乙种水果共需20元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com