Question

8．已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（4，0），点B（0，3），点P为BC边上的动点（点P不与点B、C重合），经过点O、P折叠该纸片，得点B′和折痕OP．经过点P再次折叠纸片，使点C落在直线PB′上，得点C′和折痕PQ，连接OQ．设BP=t．
（1）当t=1时，求点Q的坐标；
（2）设S_{四边形OQCB}=S，试用含有t的式子表示S；
（3）当OQ取得最小值时，求点Q的坐标．

Answer 1

分析 （1）先由翻折性质推出∠OPQ=90°，进而推出△OBP∽△PCQ，列出相似比例关系即可求得CQ，进而求得AQ的长，求得Q的坐标；
（2）由△OBP∽△PCQ，列出相似比例关系即可表示出CQ，然后根据梯形的面积公式即可求得；
（3）根据勾股定理当AQ取最小值时，OQ的值最小，由△OBP∽△PCQ，列出相似比例关系即可表示出AQ，根据二次函数的性质求得AQ取最小值即可．

解答 解：（1）如图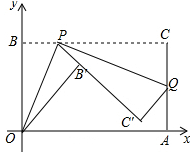：∵△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的，
∴△OB′P≌△OBP，△QC′P≌△QCP，
∴∠OPB′=∠OPB，∠QPC′=∠QPC，
∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°，
∴∠OPB+∠QPC=90°，
∵∠BOP+∠OPB=90°，
∴∠BOP=∠CPQ，
又∵∠OBP=∠C=90°，
∴△OBP∽△PCQ，
∴$\frac{OB}{PC}=\frac{BP}{CQ}$，
∵BP=1，则PC=3，
∴$\frac{3}{3}=\frac{1}{CQ}$，
∴CQ=1，
∴AQ=2，
∴Q（4，2）；
（2）∵△OBP∽△PCQ，
∴$\frac{OB}{PC}=\frac{BP}{CQ}$，
∵BP=t，BC=4，AC=3，则PC=4-t，
∴$\frac{3}{4-t}=\frac{t}{CQ}$，
∴CQ=-$\frac{1}{3}$t²+$\frac{4}{3}$t．
∴s=$\frac{1}{2}$（3-$\frac{1}{3}$t²+$\frac{4}{3}$t）×4=-$\frac{2}{3}$t²+$\frac{8}{3}$t+6（0＜t＜4）；
（3）∵△OBP∽△PCQ，
∴$\frac{OB}{PC}=\frac{BP}{CQ}$，
由题意设BP=t，AQ=m，BC=4，AC=3，则PC=4-t，CQ=3-m．
∴$\frac{3}{4-t}=\frac{t}{3-m}$，
∴m=$\frac{1}{3}$t²-$\frac{4}{3}$t+3=$\frac{1}{3}$（x-2）²+$\frac{5}{3}$（0＜t＜4）．
∵OA=4是定值，根据勾股定理当m取最小值时，OQ的值最小，
∴当t=2时，m最小值为$\frac{5}{3}$，
∴此时Q（4，$\frac{5}{3}$）．

点评 本题考查了翻折变换的性质、矩形的性质、相似三角形的判定与性质、二次函数等知识点，综合性较强，难度较大．清楚翻折前后的两个图形全等以及熟悉相似三角形的判定与性质是解决本题的关键．