
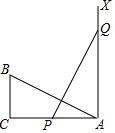
 如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP=5时,才能使△ABC与△QPA全等.
如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP=5时,才能使△ABC与△QPA全等. 分析 当AP=5时,Rt△ABC≌Rt△QPA,根据HL定理推出即可.
解答 解:当AP=5时,Rt△ABC≌Rt△QPA,
理由是:∵∠C=90°,AQ⊥AC,
∴∠C=∠QAP=90°,
当AP=5=BC时,
在Rt△ABC和Rt△QPA中,$\left\{\begin{array}{l}{AB=PQ}\\{BC=AP}\end{array}\right.$,
∴Rt△ABC≌Rt△QPA(HL),
故答案为:5.
点评 本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.


科目:初中数学 来源: 题型:解答题
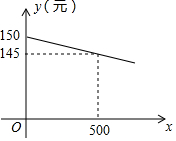 小张自主创业销售一种进价为每件20元的新型节能产品,若在国内销售,销售价格y(元/件)与月销售量x(件)的函数关系如图所示.无论销售多少,每月还需支出广告费62500元,设月利润为w1(元)(利润=销售额-成本-广告费).若在国外销售,销售价格为150元/件,受各种因素影响,成本(含进价)为40元/件,当月销量为x(件)时,每月还需缴纳$\frac{1}{100}$x2元的附加费,设月利润为w2(元)(利润=销售额-成本-附加费).
小张自主创业销售一种进价为每件20元的新型节能产品,若在国内销售,销售价格y(元/件)与月销售量x(件)的函数关系如图所示.无论销售多少,每月还需支出广告费62500元,设月利润为w1(元)(利润=销售额-成本-广告费).若在国外销售,销售价格为150元/件,受各种因素影响,成本(含进价)为40元/件,当月销量为x(件)时,每月还需缴纳$\frac{1}{100}$x2元的附加费,设月利润为w2(元)(利润=销售额-成本-附加费).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
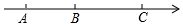 已知数轴上有A,B,C三点,它们分别表示数a,b,c,且|a+24|+|b+10|=0,又b,c互为相反数.
已知数轴上有A,B,C三点,它们分别表示数a,b,c,且|a+24|+|b+10|=0,又b,c互为相反数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com