
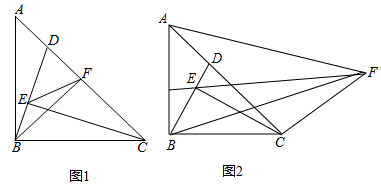
分析 (1)先过点D作DM⊥AB于点M,构造等腰直角三角形,求得DM=AM=$\frac{AD}{\sqrt{2}}$=6,再根据∠ABD=∠BCE,得出tan∠BCE=tan∠ABD=$\frac{DM}{BM}$=$\frac{3}{10}$,求得BM=20,进而根据AB=AM+BM进行计算;
(2)在CE上截取CN=BE,连接FN,先判定△BEF≌△CFN,得出△EFN是等腰直角三角形,得到EN=$\sqrt{2}$EF,再根据EN=CE-CN,得出CE-BE=$\sqrt{2}$EF;
(3)先延长BD交AC于G,作EH⊥BF于H,设CE与BF交于I,连接GI,构造等腰直角三角形和含30°角的直角三角形,再设BE=a,得出BG=2a,CE=$\sqrt{3}$a,EH=$\frac{\sqrt{2}}{2}$a=HI,GI=$\sqrt{2}$a,并求得HF=$\frac{\sqrt{2}}{2}$a+$\sqrt{6}$a,最后在Rt△EFH中,得出EF2=(7+2$\sqrt{3}$)a2,计算($\frac{EF}{EC}$)2的值即可.
解答 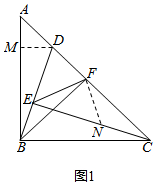 解:(1)如图1,过点D作DM⊥AB于点M,
解:(1)如图1,过点D作DM⊥AB于点M,
∵∠ABC=90°,AB=BC,
∴∠A=45°,
∴AM=DM,
∵AD=6$\sqrt{2}$,
∴DM=AM=$\frac{AD}{\sqrt{2}}$=6,
∵CE⊥BD,
∴∠BEC=90°=∠ABC,
∴∠BCE+∠EBC=90,∠EBC+∠ABD=90°,
∴∠ABD=∠BCE,
∴tan∠BCE=tan∠ABD=$\frac{DM}{BM}$=$\frac{3}{10}$,即$\frac{6}{BM}=\frac{3}{10}$,
∴BM=20,
∴AB=AM+BM=6+20=26;
(2)∵F是AB的垂直平分线上的点,
∴AF=BF,
∴∠A=∠ABF=45°,
∵∠ABC=90°,
∴∠FBC=45°,
∴∠FBC=∠FCB,且∠ABD=∠BCE,
∴BF=CF,∠EBF=∠ECF,
如图1,在CE上截取CN=BE,连接FN,
∵BF═CF,∠EBF=∠ECF,
∴△BEF≌△CFN,
∴FN=EF,∠BFE=∠CFN,
∵∠FCB=∠FBC=45°,
∴∠BFC=90°,
∴∠CFN+∠BFN=90°,
∴∠BFE+∠BFN=90°,
∴∠EFN=90°,且EF=FN,
∴△EFN是等腰直角三角形,
∴EN=$\sqrt{2}$EF,
∵EN=CE-CN,
∴CE-BE=$\sqrt{2}$EF;
(3)($\frac{EF}{EC}$)2=$\frac{7+2\sqrt{3}}{3}$.
理由:如图2,延长BD交AC于G,作EH⊥BF于H,设CE与BF交于I,连接GI,
∵∠AFB=30°,点F是AB垂直平分线上一点,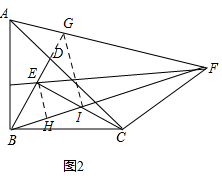
∴∠BAF=∠ABF=75°,
∵∠BDC=75°=∠ADG,∠DAG=75°-45°=30°,
∴∠AGB=75°,
∴AB=GB,
∵△ABG中,∠ABD=180°-75°×2=30°,
∴∠GBF=75°-30°=45°,且∠CBE=60°,
∵CE⊥BE,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$BG=EG,
∴IE垂直平分BG,即IG=IB,
∴∠BGI=∠IBG=45°,即GI⊥BI,
设BE=a,则BG=2a,CE=$\sqrt{3}$a,EH=$\frac{\sqrt{2}}{2}$a=HI,GI=$\sqrt{2}$a,
∵∠GFI=30°,
∴Rt△FGI中,FI=$\sqrt{3}$GI=$\sqrt{6}$a,
∴HF=$\frac{\sqrt{2}}{2}$a+$\sqrt{6}$a,
∴Rt△EFH中,EF2=EH2+HF2=($\frac{\sqrt{2}}{2}$a)2+($\frac{\sqrt{2}}{2}$a+$\sqrt{6}$a)2=(7+2$\sqrt{3}$)a2,
∴$(\frac{EF}{EC})^{2}=\frac{E{F}^{2}}{E{C}^{2}}$=$\frac{(7+2\sqrt{3}){a}^{2}}{(\sqrt{3}a)^{2}}$=$\frac{7+2\sqrt{3}}{3}$.
点评 本题是三角形的综合题,主要考查了等腰直角三角形的性质,含30°角的直角三角形的性质以及勾股定理的应用,解决问题的关键是作辅助线构造全等三角形、等腰直角三角形和30°角的直角三角形,需要运用勾股定理进行计算和推导.解题时注意:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
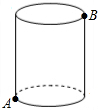 如图所示,有一圆柱,其高为12cm,它的底面周长是10cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为13 cm.
如图所示,有一圆柱,其高为12cm,它的底面周长是10cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为13 cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
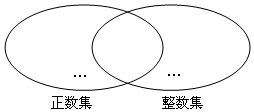 如图,两个圈分别表示负数集和整数集,请你从-3,9,0,-10%,3.14,$\frac{2}{7}$,1300这些数中,选择适当的数填在这两个圈的重叠部分.
如图,两个圈分别表示负数集和整数集,请你从-3,9,0,-10%,3.14,$\frac{2}{7}$,1300这些数中,选择适当的数填在这两个圈的重叠部分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com