
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:
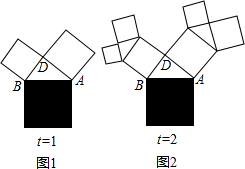 用“几何画板”中的深度迭代构造“奇妙的勾股树”动态变化,颜色也进行不断改变,在展示数学规律的同时给人一种赏心悦目的感觉.勾股树实际上是通过构造一个直角三角形,并以斜边为边长构造一个正方形(填充颜色),再依次以直角边为边长构造正方形(填充颜色),用参数t控制构造的次数,如:当t=1时,如图1所示,正方形个数为3;当t=2时,如图2所示,正方形个数为7;则当t=5时,正方形的个数为
用“几何画板”中的深度迭代构造“奇妙的勾股树”动态变化,颜色也进行不断改变,在展示数学规律的同时给人一种赏心悦目的感觉.勾股树实际上是通过构造一个直角三角形,并以斜边为边长构造一个正方形(填充颜色),再依次以直角边为边长构造正方形(填充颜色),用参数t控制构造的次数,如:当t=1时,如图1所示,正方形个数为3;当t=2时,如图2所示,正方形个数为7;则当t=5时,正方形的个数为查看答案和解析>>
科目:初中数学 来源:2011年广西南宁市中考数学模拟试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2012年中考数学模拟试卷(二十九)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2012年山东省东营市中考数学模拟试卷(四)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2012年江苏省徐州市睢宁县新世纪中学中考数学模拟试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com