
����Ŀ����ͼ��������y=��x2+6x��x�ύ�ڵ�O��A������ΪB������E�������߶Գ����ϣ���F�ڶԳ����Ҳ��������ϣ���C��x���������ϣ���EF ![]()
![]() OC������OE��CF���ı���OCFE��
OC������OE��CF���ı���OCFE��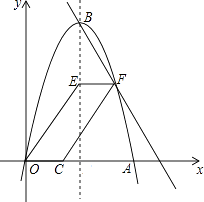
��1����B�����ꣻ
��2����tan��EOC= ![]() ʱ����Ȼ�����������ı����������������Ӧ�ĵ�F�����ꣻ
ʱ����Ȼ�����������ı����������������Ӧ�ĵ�F�����ꣻ
��3����0��tan��EOC��3ʱ������ÿһ��ȷ����tan��EOCֵ�������������ı���OCFE�����������������ı��ε����֮��Ϊ1��2ʱ����tan��EOC��
���𰸡�
��1��
�⣺��y=��x2+6x=����x��3��2+9��
��B��3��9��
��2��
�⣺�����ߵĶԳ���Ϊֱ��x=3��ֱ��x=3��x����H����ͼ��
��tan��EOC= ![]() ����tan��EOH=
����tan��EOH= ![]() ��
��
�� ![]() =
= ![]() ��
��
��EH=4��
��E��������3��4����3����4����
��y=4ʱ������x��3��2+9=4�����x1=3�� ![]() ����ȥ����x2=3+
����ȥ����x2=3+ ![]() ��
��
��y=��4ʱ������x��3��2+9=��4�����x1=3�� ![]() ����ȥ����x2=3+
����ȥ����x2=3+ ![]() ��
��
��F��������3+ ![]() ����3+
����3+ ![]() ����4��
����4��
��3��
�⣺��ͼ����ƽ���ı���OEFC��ƽ���ı���OE��F��C��ȸߣ�
���������ı��ε����֮��Ϊ1��2ʱ��OC��=2OC��
��OC=t����OC��=2t��
��F��ĺ�����Ϊ3+t��F���ĺ�����Ϊ3+2t��
����F��F��������껥Ϊ�෴����
�ੁ��3+t��3��2+9+[����3+2t��3��2+9]=0�����t1= ![]() ��t2=��
��t2=�� ![]() ����ȥ����
����ȥ����
��F��������3+ ![]() ��
�� ![]() ����
����
��E��3�� ![]() ����
����
��tan��EOC= ![]() =
= ![]() ��
��
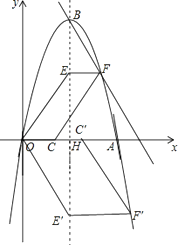
����������1�������䷽����һ��ʽ��ɶ���ʽ���ɵõ�B�����ꣻ��2�������ߵĶԳ���Ϊֱ��x=3��ֱ��x=3��x����H����ͼ���������ж���ɼ����EH���Ӷ��õ�E������Ϊ��3��4����3����4����Ȼ��ֱ���㺯��ֵΪ4�ͩ�4����Ӧ���Ա�����ֵ���ɵõ�����������F������ꣻ��3����ͼ������ƽ���ı���OEFC��ƽ���ı���OE��F��C��ȸߵõ�OC��=2OC�������OC=t����OC��=2t�����ǵõ�F��ĺ�����Ϊ3+t��F���ĺ�����Ϊ3+2t��Ȼ�����õ�F��F��������껥Ϊ�෴�����з��̩���3+t��3��2+9+[����3+2t��3��2+9]=0���ⷽ�����t��ֵ����ɵõ�F������꣬�Ӷ��õ�E�����꣬����������еĶ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ƽ��ֱ������ϵ�У�A����3����4����B��0����2����
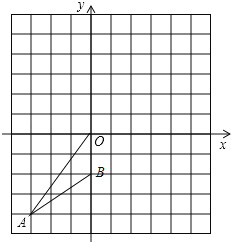
��1����OAB��O����ת180���õ���OA1B1���뻭����OA1B1����д��A1��B1�����ꣻ
��2���ж���A��B��A1��B1Ϊ������ı��ε���״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�������ع���ij������ˮ����ο��ҽ�����ߣ������ضԹ�������3000ǧ�����ϣ���3000ǧ�ˣ������������۷�����������ÿǧ��9Ԫ���ɻ����ͻ����ţ��ҷ�����ÿǧ��8Ԫ���ɹ˿��Լ���˻أ���֪�ù�˾��ӻ��ص���˾�������Ϊ5000Ԫ��
(1)�ֱ�д���ù�˾���ֹ����ĸ���y��Ԫ�����������ˮ������x��ǧ�ˣ�֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(2)���ݹ������жϣ�ѡ�����ֹ����������٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���������˶������ָ�� A��B��A��B��C �� 5 ������A �����DZ߳�Ϊ a �������Σ�C ���DZ߳�Ϊ c ��������
��1����ʽ��ʾһ�� B �������γ��ص��ܳ�������ʽ�ӻ���
��2����ʽ��ʾ�����������˶������ܳ�������ʽ�ӻ���
��3����a=4,c=2ʱ�����˶����ص��ܳ������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ű뾶��Ϊ10�İ�Բ�ε�ֽƬ��ȫ�غϵ���һ����������ֽƬ����ֱ����һ��B˳ʱ����ת30���õ���ͼ��ʾ��ͼ�Σ� ![]() ��ֱ��AB���ڵ�C�����ӵ�C��Բ��O�䣮
��ֱ��AB���ڵ�C�����ӵ�C��Բ��O�䣮 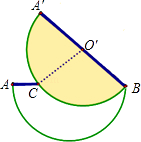
��1���� ![]() �ij���
�ij���
��2����ͼ���������Ű�Բ��ֽƬδ����������ֽƬ�ص����ֵ����S�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһ����ϵ��һ�κ���y=ax��b�Ͷ��κ���y=ax2+bx��ͼ�����Ϊ�� ��
A.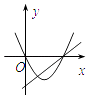
B.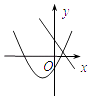
C.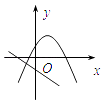
D.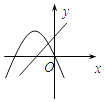
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
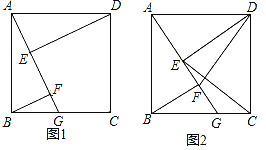
����Ŀ����ͼ1���ı���ABCD�������Σ���G��BC��������һ�㣬DE��AG�ڵ�E��BF��DE�ҽ�AG�ڵ�F��
��1����֤��DE=AF��
��2����AB=4��BG=3����AF�ij���
��3����ͼ2������DF��CE���ж��߶�DF��CE��λ�ù�ϵ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ͷ��13 800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼ�(Ԫ/��) |
�� | 24 | 36 |
�� | 33 | 48 |
(1)���̳������ס������ֿ�Ȫˮ�������䣿
(2)ȫ������500���Ȫˮ�����̳�������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
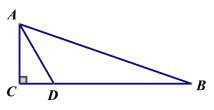
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����DΪBC����һ�㣬��BD=2AD������
����DΪBC����һ�㣬��BD=2AD������![]() ���ܳ����������ţ���
���ܳ����������ţ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com