
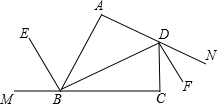
 如图,在四边形ABC中,∠A=∠C=90°,DF分别是∠B和∠D的外角平分线.求证:BE∥DF.
如图,在四边形ABC中,∠A=∠C=90°,DF分别是∠B和∠D的外角平分线.求证:BE∥DF. 分析 延长EB至G,根据四边形内角和为360°和平角的定义可得∠ABM+∠CDN=180゜,根据角平分线的性质可得∠EBM+∠CDF=90゜,根据对顶角相等和等量关系可得∠CBG+∠CDF=90゜,继而可证得∠DBG+∠BDF=180゜,根据平行线的判定可得BE∥DF.
解答 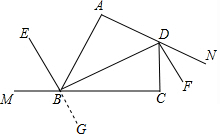 解:延长EB至G,
解:延长EB至G,
∵在四边形ABC中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,∠DBC+∠BDC=90°,
∴∠ABM+∠CDN=180゜,
∵DF分别是∠B和∠D的外角平分线,
∴∠EBM+∠CDF=90゜,
∵∠EBM=∠CBG,
∴∠CBG+∠CDF=90゜,
∴∠DBG+∠BDF=180゜,
∴BE∥DF.
点评 此题主要考查了平行线的判定,关键是掌握同旁内角互补,两直线平行.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:选择题
 如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )
如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是( )| A. | 2∠A=∠1-∠2 | B. | 3∠A=2(∠1-∠2) | C. | 3∠A=2∠1-∠2 | D. | ∠A=∠1-∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
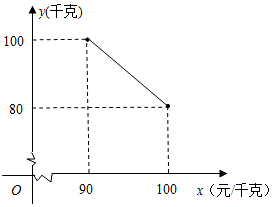 某茶叶专卖店经销一种日照绿茶,每千克成本80元,据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种日照绿茶,每千克成本80元,据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
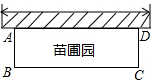 某苗圃场准备围建一个矩形新品种苗圃要求四周要围好,其中一边靠墙,另外三边用周长是32米的篱笆围成
某苗圃场准备围建一个矩形新品种苗圃要求四周要围好,其中一边靠墙,另外三边用周长是32米的篱笆围成查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com