
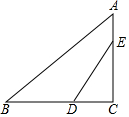
 如图,在Rt△ABC中,∠C=90°,AB=5,AC=3,点D、E分别是边BC、AC上的点,且∠EDC=∠A,将△ABC沿DE翻折,若点C恰好落在边AB上,则 DE的长为$\frac{125}{48}$.
如图,在Rt△ABC中,∠C=90°,AB=5,AC=3,点D、E分别是边BC、AC上的点,且∠EDC=∠A,将△ABC沿DE翻折,若点C恰好落在边AB上,则 DE的长为$\frac{125}{48}$. 分析 作CH⊥AB于H,根据勾股定理求出BC的长,根据三角形面积公式求出CH,根据直角三角形的性质求出CG,证明△ECD∽△BCA,得到比例式,计算即可.
解答 解:作CH⊥AB于H,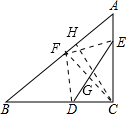
∵∠ACB=90°,AB=5,AC=3,
∴BC=4,CH=$\frac{12}{5}$,
∵∠ACB=90°,AF=FB,
∴CF=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴CG=$\frac{5}{4}$,
∵∠ECG+∠CEG=90°,∠ECG+∠GCD=90°,
∵∠GCD=∠CEG,
∵CF=BF,
∴∠CBF=∠CEG,
∴△ECD∽△BCA,
∴$\frac{DE}{AB}=\frac{CG}{CH}$,即$\frac{DE}{5}=\frac{\frac{5}{4}}{\frac{12}{5}}$,
解得DE=$\frac{125}{48}$,
故答案为:$\frac{125}{48}$
点评 本题考查的是翻折变换的性质,找准翻折变换中的对应边和对应角、正确运用相似三角形的判定和性质是解题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
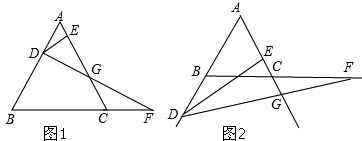
 如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB∥CD,AD∥BC,E时AB边的中点,沿EC对折长方形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.
如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB∥CD,AD∥BC,E时AB边的中点,沿EC对折长方形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com