
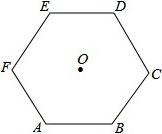
 如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.
如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.科目:初中数学 来源: 题型:
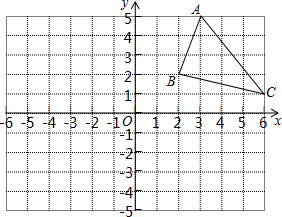 如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)
如图,△ABC的顶点坐标分别是A(2,2)、B(3,5)、C(6,1)查看答案和解析>>
科目:初中数学 来源: 题型:
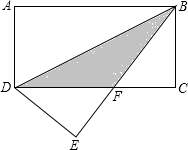 如图,将长方形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BF=5.
如图,将长方形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BF=5.查看答案和解析>>
科目:初中数学 来源: 题型:
 2010年10月26日,沪杭高铁正式通车营运,甲乙两列高速列车在A,B两地之间匀速运行,两车离A地的距离s(千米)随时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
2010年10月26日,沪杭高铁正式通车营运,甲乙两列高速列车在A,B两地之间匀速运行,两车离A地的距离s(千米)随时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
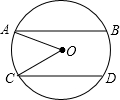 如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.
如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com