
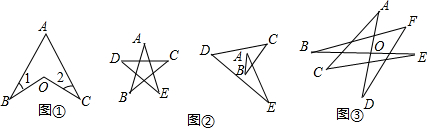
分析 (1)首先延长BO交AC于点D,可得∠BOC=∠BDC+∠2,然后根据∠BDC=∠A+∠1,判断出∠BOC=∠1+∠2+∠A即可.
(2)首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.
首先延长EA交CD于点F,EA和BC交于点G,然后根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B,再根据∠GFC+∠FGC+∠C=180°,可得x=∠A+∠B+∠C+∠D+∠E=180°,据此解答即可.
(3)根据∠BOD=80°,可得∠A+∠C+∠E=80°,∠B+∠D+∠F=80°,据此求出∠A+∠B+∠C+∠D+∠E+∠F的度数是多少即可.
解答 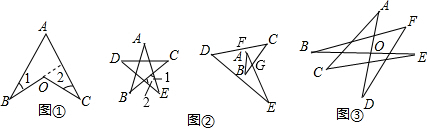 解:(1)如图①,延长BO交AC于点D,
解:(1)如图①,延长BO交AC于点D,
∵∠BOC=∠BDC+∠2,
∠BDC=∠A+∠1,
∴∠BOC=∠1+∠2+∠A.
(2)如图②,
根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图②,延长EA交CD于点F,EA和BC交于点G,
根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B,
∵∠GFC+∠FGC+∠C=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
(3)如图③,∵∠BOD=80°,
∴∠A+∠C+∠E=∠BOD=80°,
∴∠B+∠D+∠F=∠BOD=80°,
∴∠A+∠B+∠C+∠D+∠E+∠F=80°+80°=160°.
故答案为:180°;180°.
点评 此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.


科目:初中数学 来源: 题型:选择题
| A. | x2+1=0 | B. | ax2+bx+c=0 | C. | ($\frac{1}{x}$)2+($\frac{1}{x}$)-3=0 | D. | x2+3x-$\frac{{x}^{2}}{x}$=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
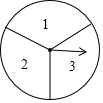 如图,一个转盘被分成3等分,每一份上各写有一个数字,随机转动转盘2次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,2次转动后组成一个两位数(若指针停在等分线上则重新转一次)
如图,一个转盘被分成3等分,每一份上各写有一个数字,随机转动转盘2次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,2次转动后组成一个两位数(若指针停在等分线上则重新转一次)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com