
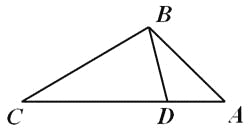
【题目】如图,△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,且点D在线段AB上,连接AE.
(1)求证:①△BCD≌△ACE;②∠DAE=90°;
(2)若AB=8,当点D在线段AB上什么位置时,四边形ADCE的周长最小?请说明并求出周长的最小值.
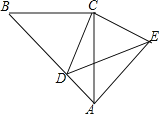
【答案】(1)①详见解析;②90°;(2)点D是AB中点时,四边形ADCE的周长最小,最小值为16.
【解析】
![]() 判断出
判断出![]() ,
,![]() ,
,![]() ,即可得出结论;
,即可得出结论;![]() 利用全等三角形的性质得出
利用全等三角形的性质得出![]() ,即可得出结论;
,即可得出结论;![]() 先判断出
先判断出![]() ,进而判断出
,进而判断出![]() 时,CD最小,即可得出结论.
时,CD最小,即可得出结论.
(1)证明:①∵△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,
∴BC=AC,CD=CE,∠BCD=∠ACE.
在△BCD和△ACE中,
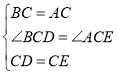 ,
,
∴△BCD≌△ACE(SAS);
②∵△ABC是等腰直角三角形,
∴∠ABC=∠BAC=45°,
由①知,△BCD≌△ACE,
∴∠ABC=∠EAC,
∴∠DAE=∠DAC+∠CAE=45°+45°=90°;
(2)∵△CDE是等腰直角三角形,
∴CD=CE,
由(1)知,△BCD≌△ACE,
∴BD=AE,
∴l四边形ADCE=AD+AE+CE+CD=AB+2CD=8+2CD,
要四边形ADCE的周长最小,
∴CD最小,
∵点D在AB上,
∴CD⊥AB时,CD最小,
∵AC=BC,
∴AD=BD.
即:点D是AB的中点,
∵△ABC是等腰直角三角形,AB=8,
∴CD最小=4,
∴l四边形ADCE最小=8+2CD最小=8+2×4=16,
即:点D是AB中点时,四边形ADCE的周长最小,最小值为16.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲两次将100斤粮食分给兄弟俩,第一次分给哥哥的粮食等于第二次分给弟弟的2倍,第二次分给哥哥的粮食是第一次分给弟弟的3倍,求两次分粮食中,哥哥、弟弟各分到多少粮食?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,连接BD,点
边上一点,连接BD,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)在(2)的条件下,如图3,若![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
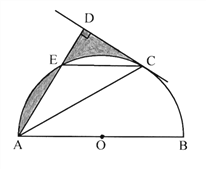
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD![]() CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com