
【题目】如图.在△ABC中,∠C=90°,AC=BC,AB=30cm,点P在AB上,AP=10cm,点E从点P出发沿线段PA以2cm/s的速度向点A运动,同时点F从点P出发沿线段PB以1cm/s的速度向点B运动,点E到达点A后立刻以原速度沿线段AB向点B运动,在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设点E、F运动的时间为t(s)(0<t<20).
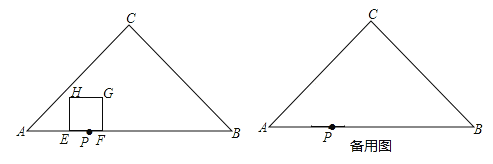
(1)当点H落在AC边上时,求t的值;
(2)设正方形EFGH与△ABC重叠部分的面积为S.①试求S关于t的函数表达式;②以点C为圆心,![]() t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
【答案】(1)t=2s或10s;(2)①S= ;②100cm2.
;②100cm2.
【解析】试题分析:(1)如图1中,当0<t≤5时,由题意AE=EH=EF,即10﹣2t=3t,t=2;如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10;
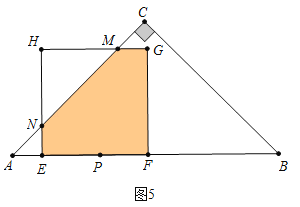
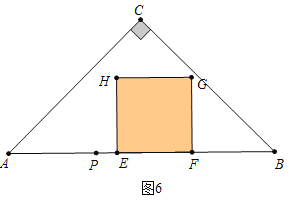
(2)分四种切线讨论a、如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2.b、如图4中,当2<t≤5时,重叠部分是五边形EFGMN.c、如图5中,当5<t<10时,重叠部分是五边形EFGMN.d、如图6中,当10<t<20时,重叠部分是正方形EFGH.分别计算即可;
②分两种情形分别列出方程即可解决问题.
试题解析:解:(1)如图1中,当0<t≤5时,由题意得:AE=EH=EF,即10﹣2t=3t,t=2
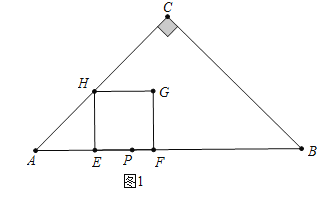
如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10.
综上所述:t=2s或10s时,点H落在AC边上.
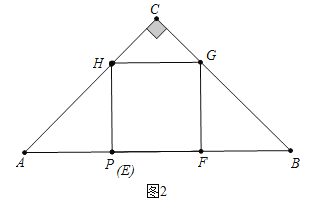
(2)①如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2
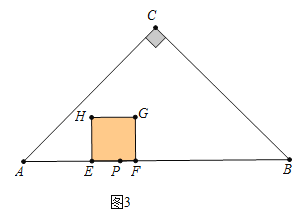
如图4中,当2<t≤5时,重叠部分是五边形EFGMN,S=(3t)2﹣![]() (5t﹣10)2=﹣
(5t﹣10)2=﹣![]() t2+50t﹣50.
t2+50t﹣50.

如图5中,当5<t<10时,重叠部分是五边形EFGMN,S=(20﹣t)2﹣![]() (30﹣3t)2=﹣
(30﹣3t)2=﹣![]() t2+50t﹣50.
t2+50t﹣50.
如图6中,当10<t<20时,重叠部分是正方形EFGH,S=(20﹣t)2=t2﹣40t+400.
综上所述:S= .
.
②如图7中,当0<t≤5时,![]() t+3t=15,解得:t=
t+3t=15,解得:t=![]() ,此时S=100cm2,当5<t<20时,
,此时S=100cm2,当5<t<20时,![]() t+20﹣t=15,解得:t=10,此时S=100.
t+20﹣t=15,解得:t=10,此时S=100.
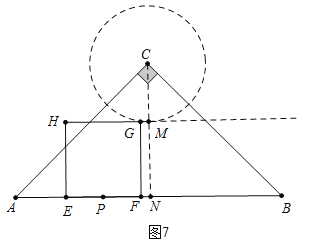
综上所述:当⊙C与GH所在的直线相切时,求此时S的值为100cm2


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.
(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;
(2)当∠B=70°时,求∠AEC的度数;
(3)当△ACE为直角三角形时,求边BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新房装修后,某居民购买家用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
垃圾桶 | 15 | ||
鞋架 | 40 | ||
字画 | a | 2 | 90 |
合计 | 5 | 185 | |
(1)居民购买垃圾桶,鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
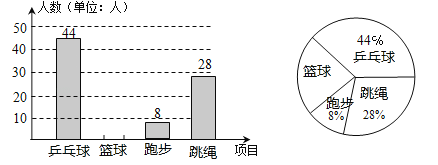
【题目】某校开展“阳光体育”活动,决定开设乒乓球、篮球、跑步、跳绳这四种运动项目,学生只能选择其中一种,为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成两张不完整的统计图,请你结合图中的信息解答下列问题:
(1)样本中喜欢篮球项目的人数百分比是 ;其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补画完整并注明人数;
(3)已知该校有1000名学生,根据样本估计全校喜欢乒乓球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:图形都是由面积为1的正方形按一定的规律组成,其中第(1)个图形中面积为1的正方形有9个,第(2)个图形中面积为1的正方形有14个,…,按此规律.则第(9)个图形中面积为1的正方形的个数为( )
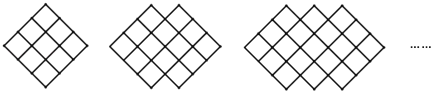
A.49B.45C.54D.50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=![]() AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8
AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8![]() ,其中正确的结论是______(只填序号).
,其中正确的结论是______(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+3)x+k2+2k=0,有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若方程的两实数根x1,x2满足x1x2﹣x12﹣x22=﹣16,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com