
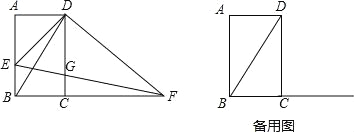
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§BC=1Θ§ΓœCBD=60ΓψΘ§ΒψE «AB±Ώ…œ“ΜΕ·ΒψΘ®≤Μ”κΒψAΘ§B÷ΊΚœΘ©Θ§Ν§Ϋ”DEΘ§ΙΐΒψDΉςDFΓΆDEΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ§Ν§Ϋ”EFΫΜCD”ΎΒψGΘ°
Θ®1Θ©«σ÷ΛΘΚΓςADEΓΉΓςCDFΘΜ
Θ®2Θ©«σΓœDEFΒΡΕ» ΐΘΜ
Θ®3Θ©…ηBEΒΡ≥ΛΈΣxΘ§ΓςBEFΒΡΟφΜΐΈΣyΘ°
ΔΌ«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωΒ±xΈΣΚΈ÷Β ±Θ§y”–Ήν¥σ÷ΒΘΜ
ΔΎΒ±yΈΣΉν¥σ÷Β ±Θ§Ν§Ϋ”BGΘ§«κ≈–Εœ¥Υ ±ΥΡ±Ώ–ΈBGDEΒΡ–ΈΉ¥Θ§≤ΔΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜ
Θ®2Θ©ΓœDEF=60ΓψΘΜ
Θ®3Θ©ΔΌy=©¹Θ®x©¹![]() Θ©2+
Θ©2+![]() Θ§
Θ§
ΓύΒ±xΈΣ![]() ±Θ§y”–Ήν¥σ÷ΒΘΜ
±Θ§y”–Ήν¥σ÷ΒΘΜ
ΔΎΥΡ±Ώ–ΈBGDE «ΤΫ––ΥΡ±Ώ–ΈΘ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΒΟΒΫΓœA=ΓœADC=ΓœDCB=90ΓψΘ§ΗυΨί”ύΫ«ΒΡ–‘÷ ΒΟΒΫΓœADE=ΓœCDFΘ§”…œύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®Ε®άμΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©Ϋβ÷±Ϋ«»ΐΫ«–ΈΒΟΒΫCD=![]() Θ§ΗυΨίΨΊ–ΈΒΡ–‘÷ ΒΟΒΫAD=BC=1Θ°AB=CD=
Θ§ΗυΨίΨΊ–ΈΒΡ–‘÷ ΒΟΒΫAD=BC=1Θ°AB=CD=![]() Θ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫ
Θ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫ![]() =
=![]() Θ§ΗυΨί»ΐΫ«Κ· ΐΒΡΕ®“εΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ§ΗυΨί»ΐΫ«Κ· ΐΒΡΕ®“εΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®3Θ©ΔΌΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫCF=3©¹![]() xΘ§ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΒΟΒΫΚ· ΐΒΡΫβΈω ΫΘ§ΗυΨίΕΰ¥ΈΚ· ΐΒΡΕΞΒψΉχ±ξΦ¥Ω…ΒΟΒΫΫα¬έΘΜΔΎΗυΨίΒ±xΈΣ
xΘ§ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΒΟΒΫΚ· ΐΒΡΫβΈω ΫΘ§ΗυΨίΕΰ¥ΈΚ· ΐΒΡΕΞΒψΉχ±ξΦ¥Ω…ΒΟΒΫΫα¬έΘΜΔΎΗυΨίΒ±xΈΣ![]() ±Θ§y”–Ήν¥σ÷ΒΘ§ΒΟΒΫBE=
±Θ§y”–Ήν¥σ÷ΒΘ§ΒΟΒΫBE=![]() Θ§CF=1Θ§BF=2Θ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡœκΒΟΒΫCG=
Θ§CF=1Θ§BF=2Θ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡœκΒΟΒΫCG=![]() Θ§”Ύ «ΒΟΒΫBE=DGΘ§”…”ΎBEΓΈDGΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
Θ§”Ύ «ΒΟΒΫBE=DGΘ§”…”ΎBEΓΈDGΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©‘ΎΨΊ–ΈABCD÷–Θ§
ΓΏΓœA=ΓœADC=ΓœDCB=90ΓψΘ§
ΓύΓœA=ΓœDCF=90ΓψΘ§
ÿDFâDEȧ
ΓύΓœA=ΓœEDF=90ΓψΘ§
ΓύΓœADE=ΓœCDFΘ§
ΓύΓςADEΓΉΓςCDFΘΜ
Θ®2Θ©ΓΏBC=1Θ§ΓœDBC=60ΓψΘ§
ΓύCD=![]() Θ§
Θ§
‘ΎΨΊ–ΈABCD÷–Θ§
ΓΏAD=BC=1Θ°AB=CD=![]() Θ§
Θ§
ΓΏΓςADEΓΉΓςCDFΘ§
Γύ![]() Θ§
Θ§
ΓΏtanΓœDEF=![]() Θ§
Θ§
Γύ![]() =
=![]() Θ§
Θ§
ΓύΓœDEF=60ΓψΘΜ
Ȯ3ȩļÿBE=xȧ
ΓύAE=![]() ©¹xΘ§
©¹xΘ§
ΓΏΓςADEΓΉΓςCDFΘ§
Γύ![]() Θ§
Θ§
ΓύCF=3©¹![]() xΘ§
xȧ
ΓύBF=BC+CF=4©¹![]() xΘ§
xȧ
Γύy=![]() BEBF=
BEBF=![]() xΘ®4©¹
xΘ®4©¹![]() xΘ©=©¹
xΘ©=©¹![]() x2+2xΘ§
x2+2xȧ
ΓΏy=©¹![]() x2+2x=©¹Θ®x©¹
x2+2x=©¹Θ®x©¹![]() Θ©2+
Θ©2+![]() Θ§
Θ§
ΓύΒ±xΈΣ![]() ±Θ§y”–Ήν¥σ÷ΒΘΜ
±Θ§y”–Ήν¥σ÷ΒΘΜ
ΔΎyΈΣΉν¥σ÷Β ±Θ§¥Υ ±ΥΡ±Ώ–ΈBGDE «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓΏΒ±xΈΣ![]() ±Θ§y”–Ήν¥σ÷ΒΘ§
±Θ§y”–Ήν¥σ÷ΒΘ§
ΓύBE=![]() Θ§CF=1Θ§BF=2Θ§
Θ§CF=1Θ§BF=2Θ§
ÿCGøBEȧ
ΓύΓςCFGΓΉΓςBFEΘ§
Γύ![]() Θ§
Θ§
ΓύCG=![]() Θ§
Θ§
ΓύDG=![]() Θ§
Θ§
ΓύBE=DGΘ§ΓΏBEΓΈDGΘ§
ΓύΥΡ±Ώ–ΈBGDE «ΤΫ––ΥΡ±Ώ–ΈΘ°




| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–‘ΥΥψ’ΐ»ΖΒΡ «
A. (a2)3ΘΫa5B. a2ΘΪ2a3ΘΫ3a5C. a6Γ¬a2ΘΫa3D. aΓΛa2ΘΫa3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΙέ≤λ»γΆΦΥυ ΨΒΡΆΦ–ΈΘ§≤Δ‘ΡΕΝœύΙΊΈΡΉ÷–≈œΔΚσΜΊ¥πœ¬Ν–Έ ΧβΘΚ
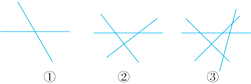
2Χθ÷±œΏœύΫΜΘ§ΉνΕύ”–1ΗωΫΜΒψΘΜ3Χθ÷±œΏœύΫΜΘ§ΉνΕύ”–3ΗωΫΜΒψΘΜ4Χθ÷±œΏœύΫΜΘ§ΉνΕύ”–6ΗωΫΜΒψΘ°
(1)8Χθ÷±œΏœύΫΜΘ§ΉνΕύ”–ΦΗΗωΫΜΒψΘΩ
(2)…η”–nΧθ÷±œΏœύΫΜΘ§ΉνΕύ”–yΗωΫΜΒψΘ§«κ”ΟΚ§nΒΡ¥ζ ΐ Ϋ±μ Ψy.
(3)Β±ΉνΕύΫΜΒψΗω ΐΈΣ4950 ±Θ§¥Υ ±÷±œΏ”–ΦΗΧθΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“‘œ¬ΥΡΉιΡΨΑτ÷–Θ§ΡΡ“ΜΉιΒΡ»ΐΧθΡήΙΜΗ’ΚΟΉω≥…÷±Ϋ«»ΐΫ«–ΈΒΡΡΨΦήΘ® Θ©
A. 7 cmȧ12 cmȧ15 cm B. 7 cmȧ12 cmȧ13 cm
C. 8 cmȧ15 cmȧ16 cm D. 3 cmȧ4 cmȧ5 cm
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Γ―OΒΡ÷±ΨΕABΒΡ≥ΛΈΣ2Θ§ΒψC‘Ύ‘≤÷ή…œΘ§ΓœCAB=30ΓψΘ§ΒψD «‘≤…œ“ΜΕ·ΒψΘ§DEΓΈABΫΜCAΒΡ―”≥ΛœΏ”ΎΒψEΘ§Ν§Ϋ”CDΘ§ΫΜAB”ΎΒψFΘ°
Θ®1Θ©»γΆΦ1Θ§Β±ΓœACD=45Γψ ±Θ§«σ÷ΛΘΚDE «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»γΆΦ2Θ§Β±ΒψF «CDΒΡ÷–Βψ ±Θ§«σΓςCDEΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥Γœζ έΦΉΓΔ““ΝΫ÷÷ΤΖ≈ΤΒΡ÷«Ρή ÷ΜζΘ§ΦΉΤΖ≈Τ ÷ΜζΒΡΫχΦέ «4000‘Σ/≤ΩΘ§ έΦέΈΣ4300‘Σ/≤ΩΘ§““ΤΖ≈ΤΒΡ έΦέΫχΦέ «2500‘Σ/≤ΩΘ§ έΦέΈΣ3000‘Σ/≤ΩΘ§ΗΟ…Χ≥ΓΦΤΜ°ΙΚΫχΝΫ÷÷ ÷Μζ»τΗ…≤ΩΘ§Ι≤–η15.5Άρ‘ΣΘ§‘ΛΦΤ»Ϊ≤Ωœζ έΚσΩ…ΜώΟΪάϊ»σΙ≤2.1Άρ‘ΣΘ§ΗΟ…Χ≥ΓΦΤΜ°ΙΚΫχΦΉΓΔ““ΝΫ÷÷ ÷ΜζΗςΕύ…Ό≤ΩΘΩΘ®ΟΪάϊ»σ=Θ® έΦέ©¹ΫχΦέΘ©ΓΝœζ έΝΩΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΑ¥œ¬ΟφΒΡ≥Χ–ρΦΤΥψΘΚ 
Β± δ»κx=100 ±Θ§ δ≥ωΫαΙϊ «299ΘΜΒ± δ»κx=50 ±Θ§ δ≥ωΫαΙϊ «466ΘΜ»γΙϊ δ»κxΒΡ÷Β «’ΐ’ϊ ΐΘ§ δ≥ωΫαΙϊ «257Θ§Ρ«Ο¥¬ζΉψΧθΦΰΒΡxΒΡ÷ΒΉνΕύ”–Θ® Θ©
A.1Ηω
B.2Ηω
C.3Ηω
D.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τ3 «ΙΊ”ΎxΒΡΖΫ≥Χx2©¹x+c=0ΒΡ“ΜΗωΗυΘ§‘ρΖΫ≥ΧΒΡΝμ“ΜΗωΗυΒ»”Ύ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com