
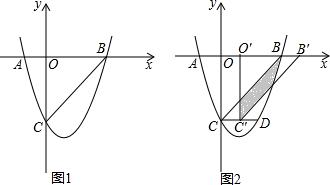
分析 (1)根据题意设抛物线交点式,待定系数法求解可得;
(2)求出点D坐标可得CD∥x轴,由B、C坐标可得∠OCB=∠CBO=∠DCB=45°,继而证△CDB≌△CQB可得CQ=CD=2,即点Q的坐标,从而求得直线BP的解析式,设抛物线上的点P(n,n2-2n-3),代入直线BP解析式可求得n的值,可得答案;
(3)①点C′在CD上运动时,即0≤t≤2时,根据:S=S△BCD-S△CC″E-S△C″DF,求解即可;
②点C′在CD延长线上运动时,即2<t≤3时,根据:S=S△GEB,求解可得.
解答 解:(1)根据题意设抛物线解析式为y=a(x+1)(x-3),
将点C(0,-3)代入,得:-3a=-3,
解得:a=1,
∴y=(x+1)(x-3)=x2-2x-3,
故答案为:y=x2-2x-3.
(2)存在,
将点D(2,m)代入抛物线解析式得:m=-3,
∴D(2,-3),
∵B(3,0),C(0,-3)
∴OC=OB,
∴∠OCB=∠CBO=45°,
如图1,设BP交y轴于点Q,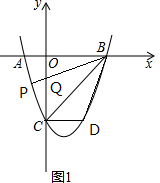
∵CD∥x轴,
∴∠DCB=∠BCQ=45°
在△CDB和△CQB中,
∵$\left\{\begin{array}{l}{∠DCB=∠BCQ}\\{BC=BC}\\{∠PBC=∠DBC}\end{array}\right.$,
∴△CDB≌△CQB(ASA)
∴CQ=CD=2,
∴点Q(0,-1),
设直线BP:y=kx-1,
点B(3,0)代入得:3k-1=0,
∴k=$\frac{1}{3}$,
∴直线BP:y=$\frac{1}{3}$x-1,
设P的坐标为(n,n2-2n-3),
代入y=$\frac{1}{3}$x-1,得:n2-2n-3=$\frac{1}{3}$n-1
解得:n=-$\frac{2}{3}$或n=3(舍去)
当n=-$\frac{2}{3}$时,n2-2n-3=-$\frac{11}{9}$
∴P(-$\frac{2}{3}$,-$\frac{11}{9}$).
(3)∵B(3,0),C(0,-3),D(2,-3),
∴求得直线BC:y=x-3,直线BD:y=3x-9,
①当0≤t≤2时,如图2:
∵由已知设C′(t,-3),B′(3+t,0)
∴求得直线C′B′:y=(x-t)-3,再联立直线BD:y=3x-9,求得F($\frac{6-t}{2}$,-$\frac{3t}{2}$),
∵∠DCB=45°
∴C′E=t
∴S=S△BCD-S△CC″E-S△C″DF=$\frac{1}{2}$×2×3-$\frac{1}{2}$×t×t-$\frac{1}{2}$×(2-t)(3-$\frac{3}{2}$t),
整理得:S=-$\frac{5}{4}$t2+3t(0≤t≤2)
②当2<t≤3时,如图3:
∵由已知设G(t,3t-9),E(t,t-3)
∴S=S△GEB=$\frac{1}{2}$[(-3t+9)-(-t+3)]×(3-t)
整理得:S=t2-6t+9(2<t≤3),
综上所述:S=$\left\{\begin{array}{l}{-\frac{5}{4}{t}^{2}+3t}&{(0≤t≤2)}\\{{t}^{2}-6t+9}&{(2<t≤3)}\end{array}\right.$.
点评 本题考查了二次函数与一次函数的图象与性质、函数图象上点的坐标特征、待定系数法、全等三角形、等腰直角三角形、图象面积计算等重要知识点.第(3)问需要分类讨论,这是本题的难点.


科目:初中数学 来源: 题型:选择题
| A. | y=-2x+1 | B. | y=-2x-1 | C. | y=-2(x-1) | D. | y=-2(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
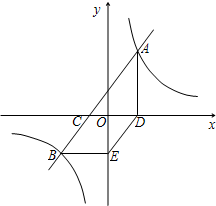 如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com