
 如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.
如图1,C地位于A,B两地之间,甲步行直接从C地前往B地;乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的$\frac{5}{2}$倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象.分析 (1)根据函数图象中点(30,2400),利用“速度=路程÷时间”可算出甲的速度,再根据甲乙速度间的关系可得出乙的速度;
(2)根据乙的速度,以及A、C两地及B、C两地间的距离,利用“时间=路程÷速度”可找出函数图象经过点(0,0)、(3,600)、(6,0)、(18,2400),按照顺序连接两点即可得出结论;
(3)设甲乙两人相遇的时间为xmin,结合(2)y2与x的函数图象可知,乙相当于比甲晚出发6分钟,依照“路程=速度×时间”可列出关于x的一元一次方程,解方程即可得出结论;
(4)结合函数图象可知:最值只有可能出现在两种情况下,乙刚到A地时或乙到B地时,分别求出两种情形下两人间的距离,再作比较即可得出结论.
解答 解:(1)甲的速度为:2400÷30=80(m/min);
乙的速度为:80×2.5=200(m/min).
故答案为:80;200.
(2)∵600÷200=3(min),
600×2÷200=6(min).
2400÷200+6=18(min).
∴y2与x的函数图象过点(0,0)、(3,600)、(6,0)、(18,2400).
画出图形如图所示.
(3)设甲乙两人相遇的时间为xmin,
依题意得:80x=200(x-6),
解得:x=10.
答:甲乙两人相遇的时间为10min.
(4)∵乙的速度>甲的速度,
∴当x=3时,乙达到A地,此时甲乙两人间距可能最远,
3×(80+200)=840(m);
当x=18时,甲乙两人间距为:
2400-80×18=960(m).
∵960>840,
∴甲乙两人相距的最远距离为960m.
故答案为:960.
点评 本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系直接计算;(2)找出拐点坐标;(3)依照数量关系列出关于x的方程;(4)找出极值,再比较极值的大小,确定最值.本题属于中档题,难度不大,解决该题型题目时,根据数量关系列出方程(或方程组)是关键.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y3>y1 | D. | y3>y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
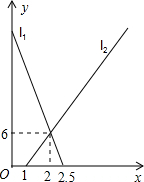 小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )
小南骑自行车从A地向B地出发,1小时后小通步行从B地向A地出发.如图,两条线段l1、l2分别表示小南、小通离B地的距离y(单位:km)与所用时间x(单位:h)之间的函数图象,根据图中的信息,则小南、小通的速度分别是( )| A. | 12 km/h,3 km/h | B. | 15km/h,3km/h | C. | 12 km/h,6 km/h | D. | 15km/h,6km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | AE=6cm | B. | sin∠EBC=0.8 | ||
| C. | 当0<t≤10时,y=0.4t2 | D. | 当t=12s时,△PBQ是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
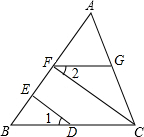 如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
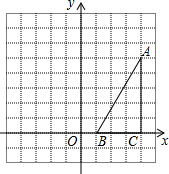 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:①画出平移后的△A′B′C′.②直接写出点A′、B′、C′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若y1<y2,则x1<x2 | |
| B. | 若y1-y2=2,则x1-x2=-1 | |
| C. | 可由直线y=2x向上平移4个单位得到 | |
| D. | 与坐标系围成的三角形面积为8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com