
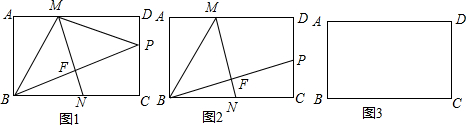
分析 (1)根据折叠的性质可知,MN垂直平分线段BP,即∠BFN=90°,由矩形的性质可得出∠C=90°=∠BFN,结合公共角∠FBN=∠CBP,即可证出△BFN∽△BCP;
(2)①在图2中,作MD、DP的垂直平分线,交于点O,以OD为半径作圆即可;
②设⊙O与BC的交点为E,连接OB、OE,由△MDP为直角三角形,可得出AP为⊙O的直径,根据BM与⊙O相切,可得出MP⊥BM,进而可得出△BMP为等腰直角三角形,根据同角的余角相等可得出∠PMD=∠MBA,结合∠A=∠PMD=90°、BM=MP,即可证出△ABM≌△DMP(AAS),根据全等三角形的性质可得出DM=AB=4、DP=AM,设DP=2a,根据勾股定理结合半径为直径的一半,即可得出关于a的方程,解之即可得出a值,再将a代入OP=2a中求出DP的长度.
解答 (1)证明:∵将矩形纸片ABCD沿直线MN折叠,顶点B恰好与CD边上的动点P重合,
∴MN垂直平分线段BP,
∴∠BFN=90°.
∵四边形ABCD为矩形,
∴∠C=90°.
∵∠FBN=∠CBP,
∴△BFN∽△BCP.
(2)解:①在图2中,作MD、DP的垂直平分线,交于点O,以OD为半径作圆即可.如图所示.
②设⊙O与BC的交点为E,连接OB、OE,如图3所示.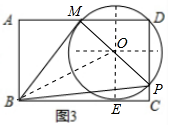
∵△MDP为直角三角形,
∴AP为⊙O的直径,
∵BM与⊙O相切,
∴MP⊥BM.
∵MB=MP,
∴△BMP为等腰直角三角形.
∵∠AMB+∠PMD=180°-∠AMP=90°,∠MBA+∠AMB=90°,
∴∠PMD=∠MBA.
在△ABM和△DMP中,$\left\{\begin{array}{l}{∠MBA=∠PMD}\\{∠A=∠PMD=90°}\\{BM=MP}\end{array}\right.$,
∴△ABM≌△DMP(AAS),
∴DM=AB=4,DP=AM.
设DP=2a,则AM=2a,OE=4-a,
BM=$\sqrt{A{B}^{2}+A{M}^{2}}$=2$\sqrt{4+{a}^{2}}$.
∵BM=MP=2OE,
∴2$\sqrt{4+{a}^{2}}$=2×(4-a),
解得:a=$\frac{3}{2}$,
∴DP=2a=3.
点评 本题考查了相似三角形的判定、矩形的性质、角的计算、切线的性质、全等三角形的判定与性质以及勾股定理,解题的关键是:(1)根据矩形的性质结合翻折的性质,找出∠C=90°=∠BFN;(2)①利用尺规作图,画出⊙O;②根据全等三角形的判定定理AAS证出△ABM≌△DMP.


科目:初中数学 来源: 题型:选择题
 实数a、b在数轴上对应点的位置如图所示,化简$\sqrt{(a-b)^{2}}$-|a+b+1|结果是( )
实数a、b在数轴上对应点的位置如图所示,化简$\sqrt{(a-b)^{2}}$-|a+b+1|结果是( )| A. | -2b-1 | B. | 2b-1 | C. | 2a-1 | D. | -2a-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
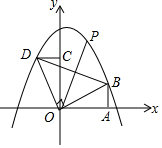 如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=-$\frac{5}{6}$x2+bx+c经过B、D两点.
如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=-$\frac{5}{6}$x2+bx+c经过B、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
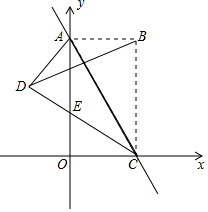 如图,在平面直角坐标系中,把矩形OABC沿对角线AC所在直线折叠,点B落在点D处,DC与y轴相交于点E,矩形OABC的边OC,OA的长是关于x的一元二次方程x2-12x+32=0的两个根,且OA>OC.
如图,在平面直角坐标系中,把矩形OABC沿对角线AC所在直线折叠,点B落在点D处,DC与y轴相交于点E,矩形OABC的边OC,OA的长是关于x的一元二次方程x2-12x+32=0的两个根,且OA>OC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{(x-1)^{2}}$ | B. | $\frac{1}{x-1}$ | C. | $\frac{3}{x-1}$ | D. | $\frac{3}{x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 65×102 | B. | 6.5×102 | C. | 6.5×103 | D. | 6.5×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com