练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为36°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走6米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，求大树CD的高度？（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）

    8.1米 【解析】试题分析：作BF⊥AE于F，则FE=BD=6米，DE=BF，设BF=x米，则AF=2.4米，在Rt△ABF中，由勾股定理得出方程，解方程求出DE=BF=5米，AF=12米，得出AE的长度，在Rt△ACE中，由三角函数求出CE，即可得出结果． 试题解析：【解析】 作BF⊥AE于F，如图所示，则FE=BD=6米，DE=BF．∵斜面AB的坡度i=1：2.4，∴AF=2.4...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：云南省双柏县2017-2018学年上学期七年级期末数学试卷 题型：解答题

    解方程： ．

    x= 【解析】试题分析：方程去分母，去括号，移项、合并同类项，化系数为1即可． 试题解析：去分母得：2x－5(3-2x)=10， 去括号得：2x-15+10x=10 移项得：2x+10x=10+15 合并同类项得：12x=25 解得： ．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：解答题

    对于实数a，b，我们可以用min{a，b}表示a，b两数中较小的数，例如min{3，－1}＝－1，min{2，2}＝2. 类似地，若函数y1、y2都是x的函数，则y＝min{y1， y2}表示函数y1和y2的“取小函数”．

    （1）设y1＝x，y2＝，则函数y＝min{x， }的图像应该是 中的实线部分．

    （2）请在下图中用粗实线描出函数y＝min{(x－2)2， (x＋2)2}的图像，并写出该图像的三条不同性质：

    ① ；

    ② ；

    ③ ；

    （3）函数y＝min{(x－4)2， (x＋2)2}的图像关于 对称．

    （1）B；（2）图见解析，正确性质见解析；（3）直线x＝1 【解析】试题分析：（1）对x分段讨论即可得出正确答案；（2）描出函数图像，根据图像解答；（3）由(x－4)2=(x＋2)2求出x的值. 【解析】 （1）当01时， ，此时y＝min{x， }的图像是y2＝的图像； 故B正确. （2）图略...

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：填空题

    若关于x的一元二次方程x2＋4x＋k﹣1＝0有实数根，则k的取值范围是____．

    k≤5 【解析】由题意得 42-4×1×（k-1）≥0, 解之得 k≤5.

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：单选题

    函数y＝3（x﹣2）2＋4的图像的顶点坐标是（ 　）

    A. （3，4） B. （﹣2，4） C. （2，4） D. （2，﹣4）

    C 【解析】函数y＝3（x﹣2）2＋4的图像的顶点坐标是（2，4）.8 故选C.

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：填空题

    如图，抛物线y=ax2+bx+c（a＞0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（4，0）在该抛物线上，则4a﹣2b+c的值为_________．

    0 【解析】试题分析：设抛物线与x轴的另一个交点是Q，∵抛物线的对称轴是过点（1，0），与x轴的一个交点是P（4，0），∴与x轴的另一个交点Q（﹣2，0），把（﹣2，0）代入解析式得：0=4a﹣2b+c，∴4a﹣2b+c=0，故答案为：0．

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：单选题

    下列四个函数图象中，当x＞0时，y随x的增大而减小的是（　　）

    A. 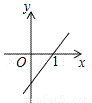B. C. D.

    B 【解析】试题分析：利用一次函数，二次函数，以及反比例函数的性质判断:当x＞0时，y随x的增大而减小的是， 故选B

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    若，则的值为__________．

    1 【解析】试题解析：∵， ∴， ∴． 故答案为1.

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    如图，△AEB≌△DFC，AE⊥CB，DF⊥BC，垂足分别为E、F，且AE=DF，若∠C=28°，则∠A=__________.

    62° 【解析】∵△AEB≌△DFC，∴∠C=∠B=28°， ∵AE⊥CB，∴∠AEB=90°，∴∠A=62°. 故答案为62°.

    查看答案和解析>>

    同步练习册答案