
����Ŀ����һ������������ABC�����ı�BC=120mm����AD=80mm����Ҫ�����ӹ��ɾ��������ʹ���ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ�
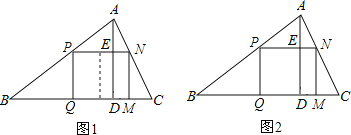
��1������˾��οɷָ���������ŷ��õ������Σ���ͼ1����ʱ�������������������ڱ߳��ֱ�Ϊ����mm��������㣮
��2�����������Ҫ�ӹ������ֻ�Ǿ��Σ���ͼ2���������˾�������������ڱ߳��Ͳ���ȷ���������������������ֵ����ﵽ������ֵʱ��������������ڱ߳���
���𰸡���1�������������������߳��ֱ�Ϊ![]() mm��
mm��![]() mm����2��S�����ֵΪ2400mm2����ʱPN=60mm��PQ=80��
mm����2��S�����ֵΪ2400mm2����ʱPN=60mm��PQ=80��![]() ��60=40��mm����
��60=40��mm����
��������
�����������1�����ھ��������������ŷ��õ�����������ɣ������PQ=ymm����PN=2ymm����֤��APN�ס�ABC�������������ε����ʽ�ɣ�
��2����PN=x����PQ��ʾ��AE�ij��ȣ�Ȼ��������������ζ�Ӧ�ߵıȵ������Ʊ��г�����ʽ����x��ʾ��PN��Ȼ����ݾ��ε������ʽ��ʽ���㣬�ٸ��ݶ��κ�������ֵ������
�⣺��1������εı߳�PN=2ymm����PQ=ymm��
��PN��BC��
���APN�ס�ABC��
��![]() ��
��
��![]() ��
��
���y=![]() ��
��
��PN=![]() ��2=
��2=![]() ��mm����
��mm����
�������������������߳��ֱ�Ϊ![]() mm��
mm��![]() mm��
mm��
��2����PN=xmm���������ɵ���APN�ס�ABC��
��![]() ��
��
��![]() ��
��
���PQ=80��![]() x��
x��
��S=PNPQ=x��80��![]() x��=��
x��=��![]() x2+80x=��
x2+80x=��![]() ��x��60��2+2400��
��x��60��2+2400��
��S�����ֵΪ2400mm2����ʱPN=60mm��PQ=80��![]() ��60=40��mm����
��60=40��mm����


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣�ֱ��x=��1�ǶԳ��ᣬ�������жϣ���b��2a=0����4a��2b+c��0����a��b+c=��9a����������3��y1������![]() ��y2���������������㣬��y1��y2��������ȷ�ĸ����ǣ� ��
��y2���������������㣬��y1��y2��������ȷ�ĸ����ǣ� ��
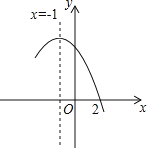
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=![]() �����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ
�����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ![]() ����EB��ED����S��APD+S��APB=1+
����EB��ED����S��APD+S��APB=1+![]() ����S������ABCD=4+
����S������ABCD=4+![]() ��������ȷ���۵�����ǣ� ��
��������ȷ���۵�����ǣ� ��

A.�٢ۢ� B���٢ڢ� C���ۢܢ� D���٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
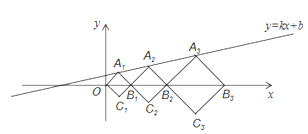
����Ŀ����ƽ��ֱ������ϵxOy�У�������A1B1C1O��A2B2C2B1��A3B3C3B2��������ͼ��ʾ�ķ�ʽ���ã���A1��A2��A3�����͵�B1��B2��B3�����ֱ���ֱ��y=kx+b��x���ϣ���֪C1��1��-1����C2��![]() ��
��![]() �������A3��������__________��
�������A3��������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ֳ�������ܳ�Ϊ110m��Χ����ǽ��ǽ��Ϊ22m��Χ����ͼ��ʾ���������������AEHG�����CDEF��������ھ���BFHG�����һ�룬��AD��Ϊxm����������ABCD�����Ϊym2��
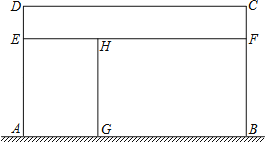
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����xΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x1 �� x2��һԪ���η���x2��2x��3=0����������x12+x22=�� ��
A.6
B.8
C.10
D.12
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com