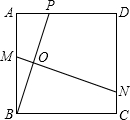精英家教网 > 初中数学 > 题目详情

如图，设AB是已知线段，在AB上作正方形ABCD；取AD的中点E，连接EB；延长DA至F，使EF=EB；以线段AF为边作正方形AFGH．则点H是AB的黄金分割点．
为什么说上述的方法作出的点H是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说．

解：设正方形ABCD的边长为2，
在Rt△AEB中，依题意，得AE=1，AB=2，
由勾股定理知EB= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
∴AH=AF=EF-AE=EB-AE= $\text{[math]}$ -1，
HB=AB-AH=3- $\text{[math]}$ ；
∴AH²=（ $\text{[math]}$ ）²=6-2 $\text{[math]}$ ，
AB•HB=2×（3- $\text{[math]}$ ）=6-2 $\text{[math]}$ ，
∴AH²=AB•HB，
所以点H是线段AB的黄金分割点．
分析：根据黄金分割点的定义，只需证明AH²=AB•HB即可．
点评：能够根据已知条件结合勾股定理求得线段的长，能够用黄金分割点的定义进行证明．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

已知：如图，点P是边长为4的正方形ABCD的边AD上一点并且不与点A、D重合，MN是线段BP的

垂直平分线，与AB、BP、CD分别交于点M、O、N，设AP=x．
（1）求BM（结果用含有x的代数式表示）；
（2）请你判断四边形MNCB的面积是否有最小值？若有最小值，求出使其面积取得最小值时的x的值并求出面积的最小值；若没有最小值，说明你的理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，已知Rt△ABC中，∠A=30°，AC=6，边长为4的等边△DEF沿射线AC运动（A、D、E、C四点共线

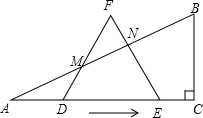），使边DF、EF与边AB分别相交于点M、N（M、N不与A、B重合）．
（1）求证：△ADM是等腰三角形；
（2）设AD=x，△ABC与△DEF重叠部分的面积为y，求y关于x的函数解析式，并写出x的取值范围；
（3）是否存在一个以M为圆心，MN为半径的圆与边AC、EF同时相切？如果存在，请求出圆的半径；如果不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．
（1）完成下面的证明：
∵MG平分∠BMN

已知

∴∠GMN=

∠BMN

角平分线的定义

同理∠GNM=

∠DNM．
∵AB∥CD

已知

，
∴∠BMN+∠DNM=

180°

∴∠GMN+∠GNM=

90°

∵∠GMN+∠GNM+∠G=

180°

∴∠G=

90°

∴MG与NG的位置关系是

MG⊥NG

（2）把上面的题设和结论，用文字语言概括为一个命题：

两平行直线被第三条直线所截，同旁内角的角平分线互相垂直

．

查看答案和解析>>

科目：初中数学 来源： 题型：044

如图所示①，已知AB是⊙O中一条固定的弦，点C是优弧的一个动点(点C不与A、B重合)．

(1)设∠ACB的角平分线与劣弧交于点P，试猜想点P在上的位置是否会随点C的运动而变化?请说明理由．

(2)如图②，设AB=8，⊙O半径为5，在(1)的条件下，四边形ACBP的面积是否是定值?若是定值，求出这个定值；若不是定值，求出四边形ACBP面积的取值范围．

查看答案和解析>>

科目：初中数学 来源：2011年山东省济南市中考数学样卷（解析版） 题型：解答题

已知：如图，点P是边长为4的正方形ABCD的边AD上一点并且不与点A、D重合，MN是线段BP的垂直平分线，与AB、BP、CD分别交于点M、O、N，设AP=x．
（1）求BM（结果用含有x的代数式表示）；
（2）请你判断四边形MNCB的面积是否有最小值？若有最小值，求出使其面积取得最小值时的x的值并求出面积的最小值；若没有最小值，说明你的理由．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学