
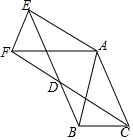
 △ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,
△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,分析 ①先利用旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则根据“SAS”证明△AEB≌△AFC,于是得到BE=CF;
②利用∠FAC=120°,AF=AC可得到∠ACF=30°,再利用AB=AC,∠BAC=45°得到∠ACB=67.5°,然后计算∠BCF;
③利用四边形ACDE是菱形得到AC∥DE,DE=AE=AC=1,则∠ABE=∠BAC=45°,于是可判断△ABE为等腰直角三角形,所以BE=$\sqrt{2}$AB=$\sqrt{2}$,然后计算BE-DE即可.
解答 ①证明:∵△ABC绕点A按顺时针方向旋转角α得到△AEF,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴AB=AC=AE=AF,
∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC,
在△AEB和△AFC中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAB=∠FAC}\\{AB=AC}\end{array}\right.$,
∴△AEB≌△AFC,
∴BE=CF;
②解:∵α=120°,
∴∠FAC=120°,
而AF=AC,
∴∠ACF=30°,
∵AB=AC,∠BAC=45°,
∴∠ACB=67.5°,
∴∠BCF=67.5°-30°=37.5°;
③解:∵四边形ACDE是菱形,
∴AC∥DE,DE=AE=AC=1,
∴∠ABE=∠BAC=45°,
而AE=AB,
∴△ABE为等腰直角三角形,
∴BE=$\sqrt{2}$AB=$\sqrt{2}$,
∴BD=BE-DE=$\sqrt{2}$-1.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了菱形的性质.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:填空题
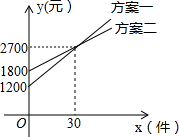 某公司推销一种产品,公司付给推销员的月报销有两种方案如图所示.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).若公司决定改进“方案二”,保持基本工资不变,每件报酬增加m元,使得当销售员销售产品达到40件时,两种方案的报酬差额不超过100元,则m的取值范围是2.5≤m≤7.5.
某公司推销一种产品,公司付给推销员的月报销有两种方案如图所示.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).若公司决定改进“方案二”,保持基本工资不变,每件报酬增加m元,使得当销售员销售产品达到40件时,两种方案的报酬差额不超过100元,则m的取值范围是2.5≤m≤7.5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.
如图点P和P1关于直线n轴对称,点P和P2关于直线m轴对称,连结P1P2交m于点A,交n于点B,连结PA和PB,若△PAB的周长为10,则P1P2=10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.
长为2,宽为a的长方形纸片(1<a<2),如图所示的方法折叠,剪下折叠所得的正方形纸片(称为第一次操作);再把剩下的长方形用同样的方法折叠,剪下折叠所得的正方形纸片(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的纸片为正方形,则操作终止.当n=3时,a的值为$\frac{6}{5}$或$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
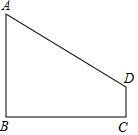 如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.
如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
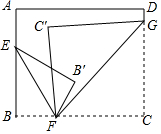 如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.
如图所示.将一张长方形纸片分别沿着EF,FG对折,使点B落在点B′,点C落在C′(B′在C′的右侧),若∠B′FC′=28°,则∠EFG的度数为104°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com