
分析 利用勾股定理可得OP的长,再由点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外?d>r;②点P在圆上?d=r;③点P在圆内?d<r;进行判断即可.
解答 解:∵OP=$\sqrt{{OC}^{2}{+PC}^{2}}$,
(1)∵PC=4,则OP=$\sqrt{{6}^{2}{+4}^{2}}$=2$\sqrt{13}$<r,
∴点P在⊙O的内部;
(2)∵PC=8,则OP=$\sqrt{{6}^{2}{+8}^{2}}$=10=r,
∴点P在⊙O上;
(3)∵PC=10,则OP=$\sqrt{{6}^{2}+1{0}^{2}}$=2$\sqrt{39}$>r,
∴点P在⊙O外部.
点评 本题主要考查了点和圆的位置关系,由勾股定理得出OP的长是解答此题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
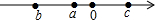 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{{(a-c)}^2}}+\sqrt{{{(b-a)}^2}}$=c-b.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,在?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com