Question

11．如图，平面直角坐标系内．四边形ABCO是矩形．AO=2$\sqrt{3}$，MN是矩形ABCO的对称轴，点M、N分别在边AO和边BC上．过点O折叠矩形．使点A落在对称轴MN上的点D处．折叠OE交对称轴MN于点F，AB于点E．

（1）求直线AF的解析式；
（2）如图2所示，当点B在线段AE的延长线上移动时，作等边△BDG，问：∠DOG的值是否发生改变？如有改变．请说明理出；如果不变，求∠BOG的值．

Answer 1

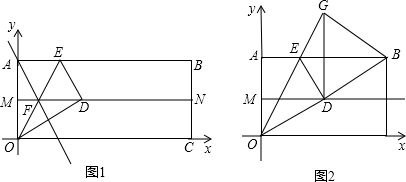
分析 （1）由折叠的性质可求得OD=OA，且M为OA中点，在Rt△OMD中可求得∠DOM=60°，则可求得∠MOF=30°，在Rt△OMF中可求得MO和MF，则可求得F点的坐标，利用待定系数法可求得直线AF的解析式；
（2）结论：∠DOG不变，∠DOG=30°．如图2中，连接AD，首先证明∠DAB=30°．再证明△ODG≌△ADB，即可解决问题．

解答 解：（1）如图1中，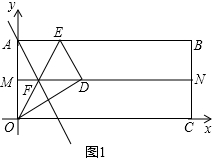

∵四边形ABCD是矩形，AM=MO，BN=NC，
∴OM=NC，OM∥NC，
∴四边形OMNC是平行四边形，
∵∠MOC=90°，
∴四边形OMNC是矩形，
∴∠NMO=90°
∵△EOD是由△EOA翻折得到，
∴OD=OA=2$\sqrt{3}$．
∵AM=MO=$\sqrt{3}$，
在Rt△DMO中，sin∠MDO=$\frac{OM}{OD}$=$\frac{1}{2}$，
∴∠MDO=30°，
∴∠MOD=60°，
∴∠MOF=$\frac{1}{2}$∠MOD=30°，
在Rt△MOF中，tan30°=$\frac{MF}{OM}$，
∴MF=1，
∴点F坐标（1，$\sqrt{3}$），设直线AF的解析式为y=kx+b，则有$\left\{\begin{array}{l}{k+b=\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$，
∴直线AF解析式为y=-$\sqrt{3}$x+2$\sqrt{3}$．

（2）结论：∠DOG不变，∠DOG=30°．
理由：如图2中，连接AD．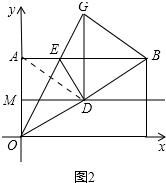

由（1）可知，OA=OD，∠AOD=60°，
∴△AOD是等边三角形，
∴∠OAD=ADO=60°，AD=OD，
∵∠OAB=90°，
∴∠DAB=30°，
∵△BDG是等边三角形，
∴DG=DB，∠GDB=60°，
∴∠ADO=∠GDB，
∴∠ODG=∠ADB，
在△ODG和△ADB中，
$\left\{\begin{array}{l}{OD=AD}\\{∠ODG=∠ADB}\\{DG=DB}\end{array}\right.$，
∴△ODG≌△ADB，
∴∠GOD=∠DAB=30°．

点评 本题考查一次函数综合题、全等三角形的判定和性质、锐角三角函数、矩形的性质等知识，解题的关键是寻找特殊三角形解决问题，学会添加常用辅助线，构造全等三角形，属于中考压轴题．