
【题目】如图①,A,E,F,C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,且AB=CD.
(1)求证:BD平分EF.
(2)若将△DEC的边EC沿AC方向移动变为图②,其余的条件不变,上述结论是否仍成立?请说明理由.

【答案】(1)证明见解析;(2)结论仍成立,理由见解析.
【解析】试题分析:(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DGE,从而得出FG=EG,即BD平分EF.
(2)结论仍然成立,同样可以证明得到.
试题解析:(1)∵AE=CF,∴AE+EF=CF+EF,
∴AF=CE.
∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°.
又∵AB=CD,∴Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
又∵∠BGF=∠DGE,
∴△BFG≌△DEG(AAS).
∴GF=GE,即BD平分EF.
(2)结论仍成立.理由如下:
∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°.
∵AE=CF,∴AE-EF=CF-EF,即AF=CE.
∵AB=CD,∴Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
又∵∠BGF=∠DGE,
∴△BFG≌△DEG(AAS).
∴GF=GE,即BD平分EF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个盒子中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色.请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在10%和15%,则箱子里蓝色球的个数很可能是 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据相关报道,开展精准扶贫户工作五年来,我国约有5500万人摆脱贫困,国家发放扶贫资金共375亿元.将375亿用科学记数法表示为( )
A. 375×107 B. 3.75×1010 C. 3.75×109 D. 37.5×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
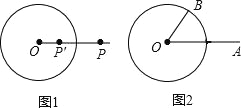
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
次数,1, 2, 3, 4, 5, 6
甲:79,78,84,81,83,75
乙:83,77,80,85,80,75
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数.
(2)写出甲、乙测验成绩的中位数.
(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一次函数y=kx+b的图象经过A(0,1),B(2,0)两点,则当x_____时,y≤0.
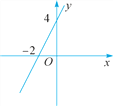
(2)如图是一次函数y=kx+b的图象,则关于x的不等式kx+b>0的解为______.
(3)若y关于x的一次函数y=mx+n的图象不经过第四象限,则m____0,n____0.
(4)设正比例函数y=mx的图象经过点A(m,4),且函数值y随x的增大而减小,则m=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com