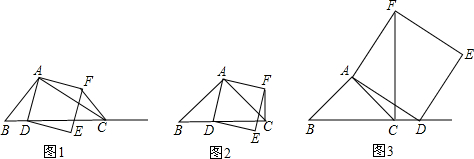
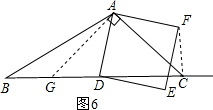
ČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻACBĪŖČń½Ē£®µćDĪŖÉäĻßBCÉĻŅ»¶Æµć£¬Į¬½ÓAD£¬ŅŌADĪŖŅ»±ßĒŅŌŚADµÄÓŅ²ą×÷Õż·½ŠĪADEF£®½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Čē¹ūAB=AC£¬”ĻBAC=90”ć£®
¢Łµ±µćDŌŚĻ߶ĪBCÉĻŹ±£ØÓėµćB²»ÖŲŗĻ£©£¬ČēĶ¼2£¬Ļ߶ĪCF”¢BDÖ®¼äµÄĪ»ÖĆ¹ŲĻµĪŖ
£¬ŹżĮæ¹ŲĻµĪŖ
£»
¢Śµ±µćDŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻŹ±£¬ČēĶ¼3£¬¢ŁÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£¬ĪŖŹ²Ć“£æ
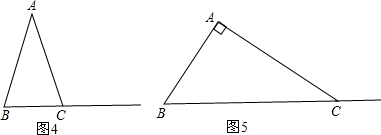
£Ø2£©¢ŁČē¹ūAB=AC£¬”ĻBAC”Ł90”ć£¬µćDŌŚÉäĻßBCÉĻŌĖ¶Æ£®ŌŚĶ¼4ÖŠĶ¬Ńł×÷³öÕż·½ŠĪADEF£¬Äć·¢ĻÖ£Ø1£©ĪŹÖŠµÄ½įĀŪŹĒ·ń³ÉĮ¢£æ²»ÓĆĖµĆ÷ĄķÓÉ£»
¢ŚČē¹ū”ĻBAC=90”ć£¬AB”ŁAC£¬µćDŌŚÉäĻßBCÉĻŌĖ¶Æ£®ŌŚĶ¼5ÖŠĶ¬Ńł×÷³öÕż·½ŠĪADEF£¬Äć·¢ĻÖ£Ø1£©ĪŹÖŠµÄ½įĀŪŹĒ·ń³ÉĮ¢£æ²»ÓĆĖµĆ÷ĄķÓÉ£»
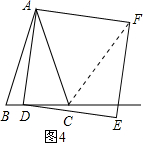
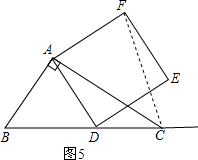
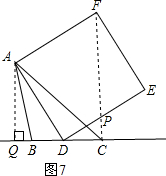
£Ø3£©ŅŖŹ¹£Ø1£©ĪŹÖŠCF”ĶBCµÄ½įĀŪ³ÉĮ¢£¬ŹŌĢ½¾æ£ŗ”÷ABCÓ¦Āś×ćµÄŅ»øöĢõ¼ž£¬£ØµćC”¢FÖŲŗĻ³żĶā£©»³öĻąÓ¦Ķ¼ŠĪ£Ø»Ķ¼²»Š“×÷·Ø£©£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø4£©ŌŚ£Ø3£©ĪŹµÄĢõ¼žĻĀ£¬ÉčÕż·½ŠĪADEFµÄ±ßDEÓėĻ߶ĪCFĻą½»ÓŚµćP£¬ÉčAC=
2£¬BC=
£¬ĒóĻ߶ĪCP³¤µÄ×ī“óÖµ£®







 Ć÷ĄķÓÉ£®
Ć÷ĄķÓÉ£®
 ČēĶ¼1£¬ADŗĶAE·Ö±šŹĒ”÷ABCµÄBC±ßÉĻµÄøßŗĶÖŠĻߣ¬µćDŹĒ“¹×ć£¬µćEŹĒBCµÄÖŠµć£¬¹ę¶Ø£ŗ¦ĖA=
ČēĶ¼1£¬ADŗĶAE·Ö±šŹĒ”÷ABCµÄBC±ßÉĻµÄøßŗĶÖŠĻߣ¬µćDŹĒ“¹×ć£¬µćEŹĒBCµÄÖŠµć£¬¹ę¶Ø£ŗ¦ĖA=