练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．下列说法正确的是（　　）
    ①内错角相等；②过直线外一点有且只有一条直线与已知直线平行；③相等的角是对顶角；④幂的乘方，底数不变，指数相加；⑤两个角的和为90°，则这两个角互补．
    A．1个B．2个C．3个D．4个

    分析 分别利用平行公理以及幂的乘方运算法则、互余的定义、对顶角的定义分别分析得出答案．

    解答 解：①两直线平行，内错角相等，故此选项错误；
    ②过直线外一点有且只有一条直线与已知直线平行，正确；
    ③相等的角不一定是对顶角，故此选项错误；
    ④幂的乘方，底数不变，指数相乘，故此选项错误；
    ⑤两个角的和为90°，则这两个角互余，故此选项错误，
    故选：A．

    点评 此题主要考查了平行公理以及幂的乘方运算、互余的定义、对顶角的定义等知识，正确把握相关定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．计算
    （1）（$\sqrt{5}$-2）（$\sqrt{5}$+2）+$\sqrt{\frac{1}{2}}$-$\sqrt{\frac{1}{3}}$×$\sqrt{48}$
    （2）-12017+（-$\frac{1}{2}$）-2-$\sqrt{\frac{1}{3}}$×$\sqrt{48}$+|1-$\sqrt{2}$|+（π-3）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．研究发现，学生对概念的接受能力y与提出概念所用的时间x（分钟）之间有如下关系：（0≤x≤30）
    提出概念所用的时间x（分钟）257101213141720
    对概念的接受能力y47.853.556.35959.859.959.858.355
    根据以上信息，回答下列问题：
    （1）表中描述的变化过程中，自变量是什么？因变量是什么？
    （2）当提出概念所用的时间为10分钟时，学生的接受能力约是多少？
    （3）当提出概念所用的时间为多少分钟时，学生的接受能力最强？
    （4）在什么时间范围内，学生的接受能力在逐渐增强？什么时间范围内，学生的接受能力在逐渐增强减弱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解下列方程组：
    （1）$\left\{\begin{array}{l}{3x+4y=7}\\{5x-y=4}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{\frac{x+y}{2}-\frac{x-y}{3}=6}\\{3（x+y）=4（x-y）}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

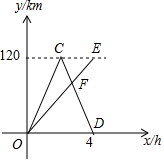    17．A，B两地相距120km，甲、乙两车同时从A地出发驶向B地，甲车到达B地后立即按原速返回．如图是它们离A地的距离y（km）与行驶时间x（h）之间的函数图象．
    （1）求甲车返回时（即CD段）y与x之间的函数解析式；
    （2）若当它们行驶了2.5h时，两车相遇，求乙车的速度及乙车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；
    （3）当两车相距30km时，甲车行驶的时间为$\frac{5}{4}$h、$\frac{35}{16}$h、$\frac{45}{16}$h．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

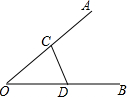    7．如图，在CD上找一点P，使得它到OA、OB的距离相等，则应找到（　　）
    A．线段CD的中点B．CD与∠AOB平分线的交点
    C．OC垂直平分线与CD的交点D．OD垂直平分线与CD的交点

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．通过学习同学们已经体会到灵活运用乘法公式给整式的乘法运算带来的方便、快捷，相信通过下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．
    例：用简便方法计算195×205．
    解：195×205
    =（200-5）（200+5）①
    =2002-52　               ②
    =39975．
    （1）例题的求解过程中，第②步变形是利用平方差公式（填乘法公式的名称）；
    （2）用简便方法计算：20172-2016×2018．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，将一个长方形条折成如图所示的形状，若已知∠1=100°，则∠2=50°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

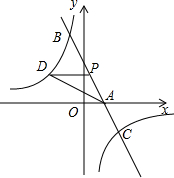    12．如图，已知一次函数y1=kx+b的图象与x轴相交于点A，与反比例函数y2=$\frac{c}{x}$的图象相交于B（-1，5），C（$\frac{5}{2}$，d）两点．点P（m，n）是一次函数y1=kx+b的图象上的动点．
    （1）求k，b的值；
    （2）直接写出y1＞y2时x的取值范围x＜-1或0＜x＜$\frac{5}{2}$；
    （3）已知-1＜m＜$\frac{3}{2}$，过点P作x轴的平行线与函数y2=$\frac{c}{x}$的图象相交于点D，试问△PAD的面积是否存在最大值？若存在，请求出面积的最大值及此时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案