
【题目】如图,函数y=kx+b和函数y=ax+m的图象,求下列不等式(组)的解集

(1)kx+b<0的解集是 ;
(2)ax+m≥0的解集是 ;
(3)kx+b<ax+m的解集是 ;
(4)ax+m>kx+b>0的解集是 ;
(5)0<ax+m<kx+b的解集是 。
【答案】(1)x<-5 ;(2)x≤2 ;(3)x<-1 ;(4) -5<x<-1;(5)-1<x<2 .
【解析】(1)观察函数图象,结合交点的坐标以及函数图象的上下关系即可得出结论;
(2)(3)(4)观察函数图象,找出函数图象与x轴交点的坐标,结合图象在x轴上下的位置关系即可得出结论.
解:(1)观察函数图象,发现:
当x<–5时,函数y=kx+b的图象在函数y=kx+b的图象的下方,
∴kx+b<0的解集是:x<–5;
(2)观察函数图象,发现:
当x≤2时,函数y=ax+m的图象在函数y=kx+b的图象的下方,
∴ax+m≥0的解集是:x≤2;
(3)观察函数图象,发现:
当x<-1时,函数y=kx+b的图象在函数y=ax+m的图象的下方,
∴kx+b<ax+m的解集为:x<-1.
答案为:x<-1.
(4)观察函数图象,发现:
当-5
∴ax+m>kx+b>0的解集为:-5
故答案为:-5
(5)观察函数图象,发现:
当-1
∴0<ax+m<kx+b的解集为:-1
“点睛”本题考查了一次函数与一元一次不等式,解题的关键是结合函数图象解集不等式,本题属于基础题,难度不大,解决该题型题目时,数形结合解决不等式(不等式组)是关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
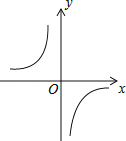
【题目】已知函数y=![]() 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(2m+1)x+m﹣3
(1)若函数图象经过原点,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值;
(3)若函数图象与y轴的交点在y轴的正半轴,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,结论错误的是( )
A. 直径相等的两个圆是等圆
B. 长度相等的两条弧是等弧
C. 圆中最长的弦是直径
D. 一条弦把圆分成两条弧,这两条弧可能是等弧
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com