练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    函数y=ax+1与y=ax2+bx+1（a≠0）的图象可能是（ ）
    A．
    B．
    C．
    D．
    【答案】分析：根据a的符号，分类讨论，结合两函数图象相交于（0，1），逐一排除；
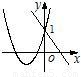
    解答：解：当a＞0时，函数y=ax2+bx+1（a≠0）的图象开口向上，函数y=ax+1的图象应在一、二、三象限，故可排除D；
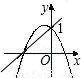
    当a＜0时，函数y=ax2+bx+1（a≠0）的图象开口向下，函数y=ax+1的图象应在一二四象限，故可排除B；
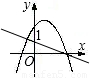
    当x=0时，两个函数的值都为1，故两函数图象应相交于（0，1），可排除A．
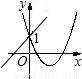
    正确的只有C．
    故选C．
    点评：应该识记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    函数y=-ax+a与y=
    a
    x
    （a≠0）在同一直角坐标系中的图象可能是（　　）
    A、精英家教网
    B、精英家教网
    C、精英家教网
    D、精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数y=ax2+bx有最大值，且图象顶点在y轴的右侧，则函数y=ax+b与y=ax2+bx的图象大致是（　　）
    A、精英家教网B、精英家教网C、精英家教网D、精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    18、当a＜0，b＞0时，函数y=ax+b与y=bx+a在同一坐标系中的图象大致是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    5、函数y=ax+b与y=ax2+bx+c的图象如图所示，则下列选项中正确的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果点（1，2）同时在函数y=ax+b与y=
    x-b
    a
    的图象上，那么a，b的值分别为（　　）

    查看答案和解析>>

    同步练习册答案