
����Ŀ����֪��������y=x2+(2m��1)x��2m(��![]() <m��
<m��![]() )��ֱ��l�Ľ���ʽΪy=(k��1)x+2m��k+2.
)��ֱ��l�Ľ���ʽΪy=(k��1)x+2m��k+2.
(1)����������y�ύ���������Ϊ��3�����������ߵĶ������ꣻ
(2)��֤������������ֱ��l�����������㣻
(3)�������߾�����(x0����4)���Ҷ�������ʵ��x������ʽx2+(2m��1)x��2m����4�������� ��k��2��x��kʱ�������ߵ���СֵΪ2k+1. ��ֱ��l�Ľ���ʽ.
���𰸡���1��y=x2+2x��3������(��1����4)����2�������������3��y =��3 x +7��y =(1+2![]() )x +3+2
)x +3+2![]()
��������
��1������������y�ύ���������Ϊ��3�����m��ֵ���ٰ������ߵĽ���ʽ�����䷽���ɵõ������ߵĶ������ꣻ
��2��������������ֱ�ߵķ���������֤���䷽����������ͬ�ĸ�������0���ɣ�
��3���������֪y��Сֵ=��4�����m��![]() ����ʱ�����ߵĶԳ���Ϊֱ�� x����1���ٷ����������Ϻ�����ͼ�����k��ֵ���ɵó�����.
����ʱ�����ߵĶԳ���Ϊֱ�� x����1���ٷ����������Ϻ�����ͼ�����k��ֵ���ɵó�����.
��1���ߣ�2m=-3,
��2m=3��
�������ߣ�y= x2+(2m��1)x��2m =x2+2x��3=( x +1)2��4��
�ඥ������Ϊ��(��1����4)
��2�������ߣ�y=x2+(2m��1)x��2m
ֱ�ߣ�y=(k��1)x+2m��k+2.
x2+(2m��k)x��4m+k��2=0
��=(2m��k)2��4(��4m+k��2)= (2m��k)2+16m��4k+8
��(2m��k)2+4(2m��k)+8m+4
=(2m��k+2)2+8m+4
��m>��![]() �� (2m��k+2)2��0
�� (2m��k+2)2��0
���>0����������ֱ��l������������.
��3���������֪y��Сֵ=��4
����![]() =��4��m��
=��4��m��![]() ��m����
��m����![]()
�ߣ�![]() <m��
<m��![]()
��m��![]() ����ʱ�����ߵĶԳ���Ϊֱ�� x����1
����ʱ�����ߵĶԳ���Ϊֱ�� x����1
�ٵ�k����1ʱ����������k��2��x��k�ϣ�ͼ���½���y��x�������С.
��ʱy��Сֵ= k2+2k��3
�� k2+2k��3=2k+1
��ã�k1��2>��1����ȥ����k2����2
�ڵ�k��2<��1<k����<��1<k <1ʱ����������k��2��x��k�ϣ� y��Сֵ=��4
�� 2k+1=��4
���ã�k=��![]() <��1 (��ȥ)��
<��1 (��ȥ)��
�۵�k��2����1����k��1ʱ����������k��2��x��k�ϣ�ͼ��������![]() ��
��![]() ���������
���������
��ʱy��Сֵ= (k��2)2+2 (k��2)��3
(k��2)2+2 (k��2)��3=2k+1��
��ã�k1��2+2![]() ��k2��2��2
��k2��2��2![]() <1 (��ȥ)��
<1 (��ȥ)��
����������ֱ��![]() ��y =��3 x +7��y =(1+2
��y =��3 x +7��y =(1+2![]() )x +3+2
)x +3+2![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ѧ����Ϊ���㾭֮�����ġ��������������й��Ŵ��㷨�Ŀ���֮�����������������м��أ���������ȸ�����࣬����֮�⣬ȸ���أ�����ᣮһȸһ�ཻ����������ƽ�����ࡢȸ��һ����ࡢȸһö���ؼ��Σ���
���ģ�������![]() ֻȸ��
ֻȸ��![]() ֻ�࣬�ֱ�۽������ú�����֮������һ���ȸ�أ����ᣮ��һֻȸ��һֻ�ཻ��λ�ö��ţ�������ȣ�
ֻ�࣬�ֱ�۽������ú�����֮������һ���ȸ�أ����ᣮ��һֻȸ��һֻ�ཻ��λ�ö��ţ�������ȣ�![]() ֻȸ��
ֻȸ��![]() ֻ������Ϊ
ֻ������Ϊ![]() ���ȸ����ÿ
���ȸ����ÿ![]() ֻ���ض��ٽ��
ֻ���ض��ٽ��
���з���������������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��D��E��F�ֱ�ΪAB��BC��AC���е㣬�����н��ۣ��١�ADF�ա�FEC�����ı���ADEFΪ���Σ���![]() ��������ȷ�Ľ�����____________.����д������ȷ���۵���ţ�
��������ȷ�Ľ�����____________.����д������ȷ���۵���ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
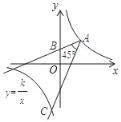
����Ŀ����ͼ��˫����![]() ������A��2��3��������AB������B��0��2����������AB��A����ʱ�뷽����ת45������˫��������C�����C�������Ϊ____.
������A��2��3��������AB������B��0��2����������AB��A����ʱ�뷽����ת45������˫��������C�����C�������Ϊ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
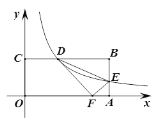
����Ŀ����ͼ������OABC�ı�OA��OC�ֱ���x�ᡢy���ϣ���B ������Ϊ(8,4)������������y=![]() (k>0)��ͼ��ֱ�BC��AB �ڵ�D��E������DE����DEF���DEB����ֱ��DE�Գƣ�����Fǡ�������߶�OA��ʱ����k��ֵ��________.
(k>0)��ͼ��ֱ�BC��AB �ڵ�D��E������DE����DEF���DEB����ֱ��DE�Գƣ�����Fǡ�������߶�OA��ʱ����k��ֵ��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
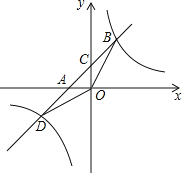
����Ŀ����֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��x�ύ�ڵ�A(��2��0)���뷴���������ڵ�һ�����ڵ�ͼ��Ľ��ڵ�B(2��n)������BO����S��AOB��4��
(1)��÷����������Ľ���ʽ��ֱ��AB�Ľ���ʽ��
(2)��ֱ��AB��˫���ߵ���һ����ΪD�㣬���ODB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
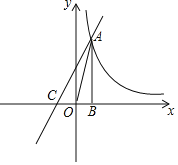
����Ŀ����ͼ����֪����������y��![]() ��ͼ����һ�����ڵ�һ��A(n��4)������A��AB��x���ڵ�B���ҡ�AOB�����Ϊ2��
��ͼ����һ�����ڵ�һ��A(n��4)������A��AB��x���ڵ�B���ҡ�AOB�����Ϊ2��
(1)��m��n��ֵ��
(2)��һ�κ���y��kx+2��ͼ����A��������x���ཻ�ڵ�C�����߶�AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx��b��ͼ���뷴��������y��![]() (x��0)��ͼ���ڵ�P(n��2)����x�ύ�ڵ�A(��4,0)����y�ύ�ڵ�C��PB��x���ڵ�B����A���B����y��Գƣ�
(x��0)��ͼ���ڵ�P(n��2)����x�ύ�ڵ�A(��4,0)����y�ύ�ڵ�C��PB��x���ڵ�B����A���B����y��Գƣ�
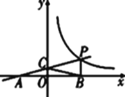
(1)��һ�κ����������������Ľ���ʽ��
(2)��֤����CΪ�߶�AP���е㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ھ���ABCD�У�AC�ǶԽ��ߣ�AB=8cm��BC=6cm����P�ӵ�A��������AC���������˶����ٶ�Ϊ2cm/s��ͬʱ����Q�ӵ�B��������BA���������˶����ٶ�Ϊ2cm/s������P��PM��AD�ڵ�M������PQ�����˶�ʱ��Ϊt��s����0��t��4��������������⣺
��1����tΪ��ֵʱ����Q���߶�AC���д����ϣ�
��2��д���ı���PQAM�����ΪS��cm2����ʱ��t�ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹS�ı���PQAM��S����ABCD=9��50�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4����tΪ��ֵʱ����APQ����ADC���ƣ�
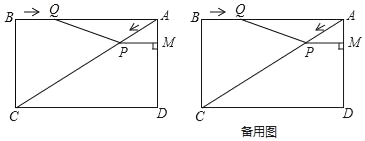
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com