
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q. 
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
【答案】
(1)解:根据题意得:PD=PE,∠DPE=90°,
∴∠APD+∠QPE=90°,
∵四边形ABCD是正方形,
∴∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠QPE,
∵EQ⊥AB,
∴∠A=∠Q=90°,
在△ADP和△QPE中,
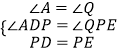 ,
,
∴△ADP≌△QPE(AAS),
∴PQ=AD=1
(2)解:∵△PFD∽△BFP,
∴ ![]() ,
,
∵∠ADP=∠EPB,∠CBP=∠A,
∴△DAP∽△PBF,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PA=PB,
∴PA= ![]() AB=
AB= ![]()
∴当PA= ![]() ,即点P是AB的中点时,△PFD∽△BFP
,即点P是AB的中点时,△PFD∽△BFP
【解析】(1)由题意得:PD=PE,∠DPE=90°,又由正方形ABCD的边长为1,易证得△ADP≌△QPE,然后由全等三角形的性质,求得线段PQ的长;(2)易证得△DAP∽△PBF,又由△PFD∽△BFP,根据相似三角形的对应边成比例,可得证得PA=PB,则可求得答案.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.

(1)求证:四边形ADCF是平行四边形;
(2)当AB与AC有何数量关系时,四边形ADCF为矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).

(1)当t为何值时,四边形PQDC是平行四边形
(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于60cm2?
(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列函数:①y=![]() ;②y=
;②y=![]() x-1;③y=-3x+1;④y=
x-1;③y=-3x+1;④y=![]() ;⑤y=-
;⑤y=-![]() (x>0);⑥y=
(x>0);⑥y=![]() (x<0).其中y随x的增大而减小的是______(填序号).
(x<0).其中y随x的增大而减小的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数的序号填到相应的横线上:
①+5,②-3,③0,④-1.414,⑤17,⑥-![]() .
.
正整数:______________________________________________________;
负分数:______________________________________________________;
负有理数:____________________________________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数图象如图所示,根据图象可得: 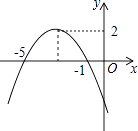
(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com