
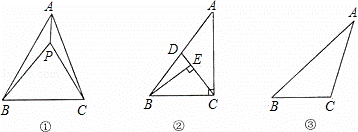
如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
(1)如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;(4分)
(2)在△ABC中,∠A<∠B<∠C.
①如图③,利用尺规作出△ABC的自相似点P(不写出作法,留作图痕迹);(3分)
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.(3分)


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:初中数学 来源: 题型:
某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元,若2元的奖品购买a件。
(1)用含a阿的代数式表示另外两种奖品的件数;
(2)请你设计购买方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
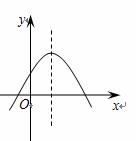
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与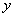 轴相交于负半轴.给出四个结论:
轴相交于负半轴.给出四个结论:
① abc<0; ②a+c=1; ③ 2a+b>0;
其中结论正确的个数为( )(2014宁波一模改编)
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
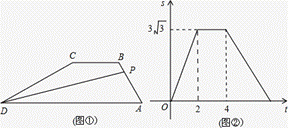
如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位: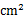 )与点P移动的时间t(单位:s)的函数关系式如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).
)与点P移动的时间t(单位:s)的函数关系式如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
在数学活动课上,王老师发给每位同学一张半径为6个单位长度的圆形纸板,要求同学们:(1)从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具,把圆形纸板分成面积相等的四部分;(2)设计的整个图案是某种对称图形.王老师给出了方案一,请你用所学的知识再设计两种方案,并完成下面的设计报告.
| 名 称 | 四等分圆的面积 | ||
| 方 案 | 方案一 | 方案二 | 方案三 |
| 选用的工具 | 带刻度的三角板 | ||
|
|
|
|
|
| 简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. | ||
| 指出对称性 | 既是轴对称图形又是中心对称图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com