
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

【答案】![]()
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣![]() )(m<0),则E(0,﹣
)(m<0),则E(0,﹣![]() ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣![]() ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣![]() ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣![]() 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
![]()
故答案为:2![]() .
.
【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣![]() ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
【题型】填空题
【结束】
18
【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
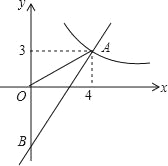
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用1500元人民币购进某种水果销售,过了一周时间,又用3400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于900元,则每千克这种水果的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张对面互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论不正确的有( ).
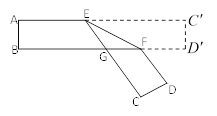
A.![]() B.∠AEC=148°C.∠BGE=64°D.∠BFD=116°
B.∠AEC=148°C.∠BGE=64°D.∠BFD=116°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解答问题:
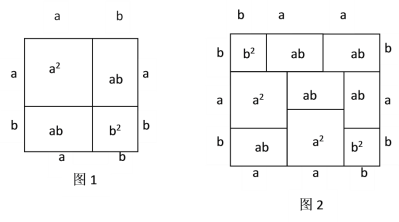
七年级第一学期课本中有这样一个思考题:“你能根据图1中的图形来说明完全平方公式吗?”说明如下:
图1中的面积可以表示为![]() ;图1中的面积又可以表示为
;图1中的面积又可以表示为![]() ;所以这个图形说明了完全平方公式
;所以这个图形说明了完全平方公式![]() 除了完全平方公式可以用图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示.
除了完全平方公式可以用图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示.
(1)请写出图2所表示的代数恒等式:__________________________________;
(2)请画一个图形,使它的面积能表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com