
 如图,∠DAB+∠CDA=180°,∠ABC=∠EAD,直线AB与CD平行吗?直线AD与直线BC呢?为什么?
如图,∠DAB+∠CDA=180°,∠ABC=∠EAD,直线AB与CD平行吗?直线AD与直线BC呢?为什么? 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
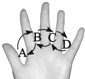 如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,5,6,…,当字母C第101次出现时,恰好数到的数是303.
如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,5,6,…,当字母C第101次出现时,恰好数到的数是303.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com