
【题目】某方便面厂10月份生产方便面100吨,这样1至10月份生产量恰好完成全年的生产任务,为了满足市场需要,计划到年底再生产231吨方便面,这样就超额全年生产任务的21%,则11、12月的月平均增长率为( )
A.10%
B.31%
C.13%
D.11%
科目:初中数学 来源: 题型:
【题目】如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.
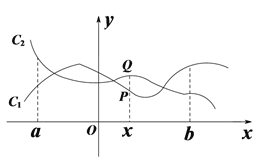
例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2并研究该函数在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,说明理由;
(2)若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
(3)若函数y =![]() 与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
其中说法正确的是( )

A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com